题目内容
已知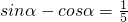 ,且α是第三象限的角,
,且α是第三象限的角,
计算:
(1)sinα+cosα;
(2)tan2α.
解:(1)∵α是第三象限的角,
∴cosα<0,sinα<0
∴sinα+cosα<0(2分)
∵sinα-cosα= ①,
①,
∴1-2sinαcosα= ,2sinαcosα=
,2sinαcosα= (4分)
(4分)
∴1+2sinαcosα= 得:
得:
(sinα+cosα)2= ;
;
∴sinα+cosα=- ②(7分)
②(7分)
(2)由①、②联立方程组可得sinα=- ,(9分)
,(9分)
∴tanα= (10分)
(10分)
∴tan2α=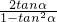 =
= (12分)
(12分)
分析:(1)由α是第三象限的角,可知cosα<0,sinα<0,从而可求得sinα+cosα;
(2)由①②可求得tanα,利用二倍角的正切即可求得答案.
点评:本题考查同角三角函数间的基本关系,考查方程思想,考查二倍角的正弦与正切公式,属于中档题.
∴cosα<0,sinα<0
∴sinα+cosα<0(2分)
∵sinα-cosα=
 ①,
①,∴1-2sinαcosα=
 ,2sinαcosα=
,2sinαcosα= (4分)
(4分)∴1+2sinαcosα=
 得:
得:(sinα+cosα)2=
 ;
;∴sinα+cosα=-
 ②(7分)
②(7分)(2)由①、②联立方程组可得sinα=-
 ,(9分)
,(9分)∴tanα=
 (10分)
(10分)∴tan2α=
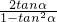 =
= (12分)
(12分)分析:(1)由α是第三象限的角,可知cosα<0,sinα<0,从而可求得sinα+cosα;
(2)由①②可求得tanα,利用二倍角的正切即可求得答案.
点评:本题考查同角三角函数间的基本关系,考查方程思想,考查二倍角的正弦与正切公式,属于中档题.

练习册系列答案
相关题目
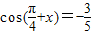 ,且x是第三象限角,则
,且x是第三象限角,则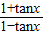 的值为( )
的值为( )