题目内容
随着田径110米栏运动员刘翔的崛起,大家对这项运动的关注度也大大提高,有越来越多的人参与到了这项运动中,为了解某班学生对了解110米栏运动是否与性别有关,对本班同学进行了问卷调查,得到了如下的列联表:| 了解110米栏 | 了解110米栏 | 合计 | |
| 男生 | 22 | 8 | 30 |
| 女生 | 8 | 12 | 20 |
| 合计 | 30 | 20 | 50 |
(2)在上述抽取的5人中选2人,求至少有一人是男生的概率;
(3)你有95%还是99%的把握认为是否了解110米栏与性别有关?并证明你的结论.
附:k2=
 ,
,| P(k2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
【答案】分析:(1)确定在不了解110米栏运动的学生中抽5人抽取的比例,即可求男、女生各抽取多少人;
(2)利用对立事件概率求解公式,即可求解;
(2)计算k2的值,与临界值比较,即可得到结论.
解答:解:(1)在不了解110米栏运动的学生中抽5人,则抽取比例为 =
=
∴男生应该抽取8× =2人,女生应该抽取
=2人,女生应该抽取 =3人;
=3人;
(2)上述抽取的5人中选2人,共有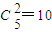 种方法,则至少有一人是男生的概率为1-
种方法,则至少有一人是男生的概率为1-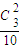 =
= ;
;
(3)∵k2= ≈5.56≥3.841
≈5.56≥3.841
∴我们有95%的把握认为了解110米栏与性别有关.
点评:本题考查分层抽样,考查概率的计算,考查独立性检验知识,考查学生的计算能力,属于中档题.
(2)利用对立事件概率求解公式,即可求解;
(2)计算k2的值,与临界值比较,即可得到结论.
解答:解:(1)在不了解110米栏运动的学生中抽5人,则抽取比例为
 =
=
∴男生应该抽取8×
 =2人,女生应该抽取
=2人,女生应该抽取 =3人;
=3人;(2)上述抽取的5人中选2人,共有
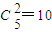 种方法,则至少有一人是男生的概率为1-
种方法,则至少有一人是男生的概率为1-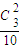 =
= ;
;(3)∵k2=
 ≈5.56≥3.841
≈5.56≥3.841∴我们有95%的把握认为了解110米栏与性别有关.
点评:本题考查分层抽样,考查概率的计算,考查独立性检验知识,考查学生的计算能力,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目