题目内容
设α,β均为钝角,sinα=
,cosβ=-
,则α+β=( )
| ||
| 5 |
3
| ||
| 10 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:通过α、β均为钝角,sinα=
,cosβ=-
,求出cosα=-
,sinβ=
,然后求出cos(α+β)的值,即可根据α、β的范围,求出α+β的值.得到选项.
| ||
| 5 |
3
| ||
| 10 |
2
| ||
| 5 |
| ||
| 10 |
解答:解:∵α、β为钝角
又∵sinα=
,cosβ=-
∴cosα=-
,sinβ=
,
∴cos(α+β)=cosαcosβ-sinαsinβ=
又 π<α+β<2π
∴α+β=
故选A
又∵sinα=
| ||
| 5 |
3
| ||
| 10 |
∴cosα=-
2
| ||
| 5 |
| ||
| 10 |
∴cos(α+β)=cosαcosβ-sinαsinβ=
| ||
| 2 |
又 π<α+β<2π
∴α+β=
| 7π |
| 4 |
故选A
点评:本题是基础题,考查两角和的余弦函数,解题中去cos(α+β)好于sin(α+β),因为三、四象限,正弦都是负数,余弦值不同,这是本题的一个陷阱,也学生容易出错的地方,是好题,常考题.

练习册系列答案
相关题目
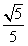 ,cosβ=
,cosβ=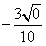 ,则α+β=( )。
,则α+β=( )。