题目内容
已知函数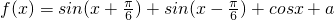 的最大值为1.
的最大值为1.
(1)求常数a的值;(2)求使f(x)≥0成立的x的取值集合.
解: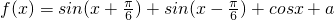
=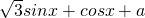
=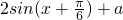
(1)f(x)的最大值为1∴1=2+a∴a=-1
(2)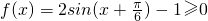 ,∴
,∴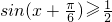
∴
∴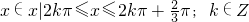
分析:先根据两角和与差的正弦公式展开合并,对函数f(x)进行化简.
(1)根据函数f(x)的最大值为1可求出a的值.
(2)将a的值代入可确定函数f(x)的解析式,然后令f(x)≥0结合正弦函数的性质可得到 ,进而可求出x的范围.
,进而可求出x的范围.
点评:本题主要考查两角和与差的正弦公式和正弦函数的性质.考查队基础知识的简单应用.三角函数是高考考查的重要考点,要强化复习.
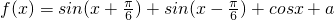
=
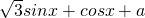
=
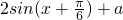
(1)f(x)的最大值为1∴1=2+a∴a=-1
(2)
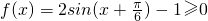 ,∴
,∴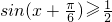
∴

∴
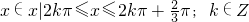
分析:先根据两角和与差的正弦公式展开合并,对函数f(x)进行化简.
(1)根据函数f(x)的最大值为1可求出a的值.
(2)将a的值代入可确定函数f(x)的解析式,然后令f(x)≥0结合正弦函数的性质可得到
 ,进而可求出x的范围.
,进而可求出x的范围.点评:本题主要考查两角和与差的正弦公式和正弦函数的性质.考查队基础知识的简单应用.三角函数是高考考查的重要考点,要强化复习.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的最大值为1.
的最大值为1. 的最大值为1.
的最大值为1. 的值;(2)求使
的值;(2)求使 成立的x的取值集合.
成立的x的取值集合. 的最大值为1,最小值为
的最大值为1,最小值为 ,则函数
,则函数 的最大值为
的最大值为  的最大值为
的最大值为 .
. 的值;
的值; 成立的
成立的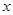 的取值范围.
的取值范围.