题目内容
考察下列一组不等式:
将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为
分析:将题目中的三个式子变形得22+1+52+1>22•51+21•52(1) 23+1+53+1>23•51+21•53(2)22+
+52+
>22•5
+2
•52(3)会发现指数满足的条件,可类比得到2m+n+5m+n>2m5n+2n5m,使式子近一步推广得am+n+bm+n>ambn+anbm(a,b>0,a≠b,m,n>0)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:22+1+52+1>22•51+21•52(1)
23+1+53+1>23•51+21•53(2)
22+
+52+
>22•5
+2
•52(3)
观察(1)(2)(3)式指数会发现规律,故答案为am+n+bm+n>ambn+anbm(a,b>0,a≠b,m,n>0)
23+1+53+1>23•51+21•53(2)
22+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
观察(1)(2)(3)式指数会发现规律,故答案为am+n+bm+n>ambn+anbm(a,b>0,a≠b,m,n>0)
点评:本题考查了归纳推理,根据一类事物的部分对象具有某种性质,推出这类事物的所有对象都具有这种性质的推理.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
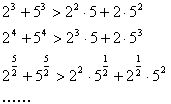 将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为 ___。
将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为 ___。