题目内容
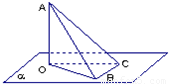
 如图,AO⊥平面α,点O为垂足,BC?平面α,BC⊥OB,若∠ABO=
如图,AO⊥平面α,点O为垂足,BC?平面α,BC⊥OB,若∠ABO=| π |
| 4 |
| π |
| 6 |
分析:结合题意并且根据三垂线定理可得:BC⊥AB.设OB=2,所以AB=2
,BC=
,在△ABC中tan∠BAC=
=
,进而根据三角函数关系求出角的余弦值.
| 2 |
2
| ||
| 3 |
| BC |
| AB |
| ||
| 6 |
解答:解:因为AO⊥平面α,BC?平面α,BC⊥OB,
所以根据三垂线定理可得:BC⊥AB.
设OB=2,
因为∠ABO=
,∠COB=
,
所以OA=2,AB=2
,BC=
,
所以在△ABC中有BC⊥AB,并且AB=2
,BC=
,
所以tan∠BAC=
=
,
所以cos∠BAC=
.
故答案为:
.
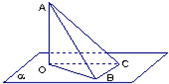
所以根据三垂线定理可得:BC⊥AB.
设OB=2,
因为∠ABO=
| π |
| 4 |
| π |
| 6 |
所以OA=2,AB=2
| 2 |
2
| ||
| 3 |
所以在△ABC中有BC⊥AB,并且AB=2
| 2 |
2
| ||
| 3 |
所以tan∠BAC=
| BC |
| AB |
| ||
| 6 |
所以cos∠BAC=
| ||
| 7 |
故答案为:
| ||
| 7 |
点评:解决此类问题的关键是熟练掌握几何体的结构特征,根据题中的条件得到线段的长度关系,进而利用解三角形的有关知识求解线线角问题.

练习册系列答案
相关题目
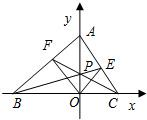 如图,在平面直角坐标系xoy中,设三角形ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)在线段AO上的一点(异于端点),这里a,b,c,p均为非零实数,设直线BP,CP分别与边AC,AB交于点E,F.
如图,在平面直角坐标系xoy中,设三角形ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)在线段AO上的一点(异于端点),这里a,b,c,p均为非零实数,设直线BP,CP分别与边AC,AB交于点E,F.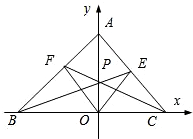 如图,在平面直角坐标系xoy中,设三角形ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)在线段AO上的一点(异于端点),这里a,b,c,p均为非零实数,设直线BP,CP分别与边AC,AB交于点E,F,某同学已正确求得直线OE的方程为
如图,在平面直角坐标系xoy中,设三角形ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)在线段AO上的一点(异于端点),这里a,b,c,p均为非零实数,设直线BP,CP分别与边AC,AB交于点E,F,某同学已正确求得直线OE的方程为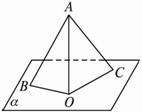
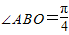 ,
,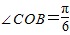 ,则cos∠BAC= .
,则cos∠BAC= .