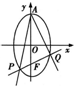题目内容
已知椭圆C:x2+| y2 |
| m |
| ||
| 2 |
(1)求椭圆C的方程;
(2)设P为椭圆上一点,且满足
| OA |
| OB |
| OP |
| PA |
| PB |
| 3 |
分析:(1)由题知a2=m,b2=1,∴c2=m-1,且离心率为
,得m=4.由此能求出椭圆的方程.
(2)当l的斜率不存在时,|
-
|=|
|=4>
,不符合条件.设l的斜率为k,则l的方程为y=kx+3.设A(x1,y1),B(x2,y2),P(x0,y0),联立l和椭圆的方程:
,消去y,整理得(4+k2)x2+6kx+5=0,再由根的判别式和韦达定理进行求解.
| ||
| 2 |
(2)当l的斜率不存在时,|
| PA |
| PB |
| AB |
| 3 |
|
解答:解:(1)由题知a2=m,b2=1,∴c2=m-1
∴e=
=
=
,解得m=4.
∴椭圆的方程为x2+
=1.(4分)
(2)当l的斜率不存在时,|
-
|=|
|=4>
,不符合条件.(5分)
设l的斜率为k,则l的方程为y=kx+3.设A(x1,y1),B(x2,y2),P(x0,y0),联立l和椭圆的方程:
,.消去y,整理得(4+k2)x2+6kx+5=0,
∴△=(6k)2-4×(4+k2)×5=16k2-80>0,解得k2>5.且x1+x2=-
,x1x2=
,
∴|
-
|=|
|=
•
=
由已知有
<
整理得13k4-88k2-128<0,解得-
<k2<8,
∴5<k2<8.(9分)
∵
+
=λ
,即(x1,y1)+(x2,y2)=λ(x0,y0),
∴x1+x2=λx0,y1+y2=λy0
当λ=0时,x1+x2=-
=0,y1+y2=k(x1+x2)+6=
=0,显然,上述方程无解.
当λ≠0时,x0=
=-
,y0=
=
.
∵P(x0,y0)在椭圆上,即
+
=1,
化简得λ2=
.由5<k2<8,可得3<λ2<4,
∴λ∈(-2,-
)∪(
,2).即λ的取值范围为(-2,-
)∪(
,2).(12分)
∴e=
| c |
| a |
| ||
|
| ||
| 2 |
∴椭圆的方程为x2+
| y2 |
| 4 |
(2)当l的斜率不存在时,|
| PA |
| PB |
| AB |
| 3 |
设l的斜率为k,则l的方程为y=kx+3.设A(x1,y1),B(x2,y2),P(x0,y0),联立l和椭圆的方程:
|
∴△=(6k)2-4×(4+k2)×5=16k2-80>0,解得k2>5.且x1+x2=-
| 6k |
| 4+k2 |
| 5 |
| 4+k2 |
∴|
| PA |
| PB |
| AB |
| 1+k2 |
| (x1+x2)2-4x1x2 |
4
| ||
| 4+k2 |
由已知有
4
| ||
| 4+k2 |
| 3 |
| 16 |
| 13 |
∴5<k2<8.(9分)
∵
| OA |
| OB |
| OP |
∴x1+x2=λx0,y1+y2=λy0
当λ=0时,x1+x2=-
| 6k |
| 4+k2 |
| 24 |
| 4+k2 |
当λ≠0时,x0=
| x1+x2 |
| λ |
| 6k |
| λ(4+k2) |
| y1+y2 |
| λ |
| 24 |
| λ(4+k2) |
∵P(x0,y0)在椭圆上,即
| x | 2 0 |
| y02 |
| 4 |
化简得λ2=
| 36 |
| 4+k2 |
∴λ∈(-2,-
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查圆锥曲线和直线 的位置关系和应用,解题时要注意公式的灵活运用.

练习册系列答案
相关题目
 如图所示,已知椭圆C:
如图所示,已知椭圆C: