Question

Ａ设实数x，y，m，n满足x²+y²=1，m²+n²=3那么mx+ny的最大值是（　　　　　）

Ａ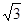．　　　　　　Ｂ．2　　　　　Ｃ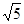．　　　　　　Ｄ． 

 

Answer 1

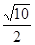
【答案】

A

【解析】

试题分析：解法一：设x=sinα，y=cosα，m=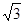sinβ，n=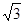cosβ，其中α，β∈∈（0°，180°）其他略。

解法二、m²+n²=3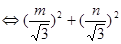＝1∴2＝x²+y²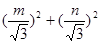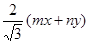＋ ≥∴mx+ny≤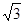。故选A。

考点：本题主要考查均值定理的应用。

点评：从题目的条件看，可有两种思路，一是利用函数思想，实施三角换元，二是应用均值定理。特别注意，特别注意，应用均值定理需满足“一正、二定、三相等”。