题目内容
某水库堤坝年久失修,发生了渗水现象,经测算坝面每渗水1m2的直接经济损失约为250元,当发现时已有200m2的坝面每渗水,且渗水面积以每天4m2的速度扩散,当地政府在发现的同时,立即组织民工进行抢修,假定每位民工平均每天可抢修渗水面积2m2,为此政府需支出服装补贴费每人400元,劳务费每人每天150元,所消耗的维修材料等费用每人每天150元,若安排x名民工参与抢修,抢修完成需用n天.(1)写出n天关于x的函数关系式;
(2)应安排多少名民工参与抢修,才能使总损失最少.(总损失=渗水损失+政府支出)
【答案】分析:(1)根据发现时已有200m2的坝面渗水,渗水现象正在以每天4m2的速度扩散及每个工人平均每天可抢修渗水面积2m2,共派去x名工人,抢修完成共用n天,可得2nx=200+4n,进而求出n关于x的函数关系式.
(2)由(1)结论,结合基本不等式,我们易求出要使总损失最小时的工人分派方案.
解答:解:(1)由题意得2nx=200+4n,所以n= ,x≥3,x∈N+;
,x≥3,x∈N+;
(2)设总损失为y,则y=250×(200+4n)+400x+nx×(150+150)=80800+400(x-2)+
≥80800+2×20×400=96800
当且仅当400(x-2)=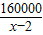 时,即x=22时,等号成立
时,即x=22时,等号成立
∴应安排22名民工参与抢修,才能使总损失最少.
点评:本题考查函数模型的构建,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.
(2)由(1)结论,结合基本不等式,我们易求出要使总损失最小时的工人分派方案.
解答:解:(1)由题意得2nx=200+4n,所以n=
 ,x≥3,x∈N+;
,x≥3,x∈N+;(2)设总损失为y,则y=250×(200+4n)+400x+nx×(150+150)=80800+400(x-2)+

≥80800+2×20×400=96800
当且仅当400(x-2)=
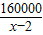 时,即x=22时,等号成立
时,即x=22时,等号成立∴应安排22名民工参与抢修,才能使总损失最少.
点评:本题考查函数模型的构建,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目