题目内容
等差数列{an} 中,a3 =2,则该数列的前5项的和为
| A.10 | B.16 | C.20 | D.32 |
A
解析试题分析:根据等差中项的性质可知2a3=a1+a5,代入等差数列的求和公式即可求得答案.因为
2a3=a1+a5,则可知 ,故答案为0.故选A.
,故答案为0.故选A.
考点:等差数列的前n项的和.
点评:本题主要考查了等差数列的前n项的和.解题的关键是利用了等差中项的性质.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知 为等差数列,若
为等差数列,若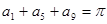 ,则
,则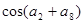 的值为
的值为
A.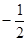 | B.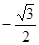 | C.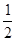 | D.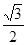 |
已知数列{an}满足a1=0,an+1= (n∈N*),则a20等于( )
(n∈N*),则a20等于( )
| A.0 | B.- |
C. | D.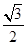 |
等差数列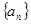 前
前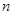 项和为
项和为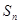 ,
,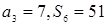 ,则公差d的值为
,则公差d的值为
| A.2 | B.3 | C.-3 | D.4 |
已知等差数列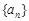 公差
公差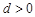 ,前n项和为
,前n项和为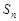 .则“
.则“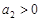 ”是“数列
”是“数列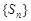 为递增数列”的
为递增数列”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充也不必要条件 |
已知数列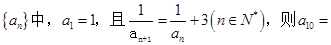
| A.28 | B.33 | C.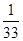 | D.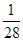 |
已知等差数列 中,前
中,前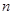 项和为
项和为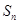 ,若
,若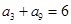 ,则
,则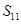 等于( )
等于( )
| A.12 | B.33 | C.66 | D.11 |
首项为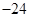 的等差数列,从第10项开始为正数,则公差
的等差数列,从第10项开始为正数,则公差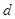 的取值范围是( )
的取值范围是( )
A.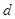 > >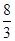 | B.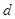 >3 >3 | C.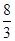 ≤ ≤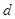 <3 <3 | D.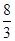 < <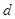 ≤3 ≤3 |
首项为 的等差数列,从第10项起开始为正数,则公差d的取值范围是
的等差数列,从第10项起开始为正数,则公差d的取值范围是
A.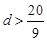 | B.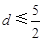 | C.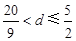 | D.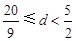 |