题目内容
a，b∈R，命题P：a＞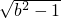
；命题q：直线y=ax+b与圆x2+y2=1相交，则p 是q的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
A
分析：分别求出命题p和q的等价条件，利用充分必要的定义进行判断；
解答：命题p，a＞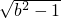
等价于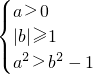
，
命题q，直线y=ax+b与圆x2+y2=1相交，圆心到直线的距离小于1，
等价于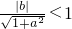
即a2＞b2-1，显然由命题p可得命题q，反之不真；
∴p 是q充分不必要条件，
故选A；
点评：此题主要考查充分必要条件的定义，是一道基础题；
分析：分别求出命题p和q的等价条件，利用充分必要的定义进行判断；
解答：命题p，a＞
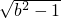
等价于
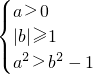，命题q，直线y=ax+b与圆x2+y2=1相交，圆心到直线的距离小于1，
等价于
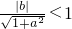即a2＞b2-1，显然由命题p可得命题q，反之不真；∴p 是q充分不必要条件，
故选A；
点评：此题主要考查充分必要条件的定义，是一道基础题；
练习册系列答案
教材全解字词句篇系列答案
相关题目
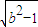；命题q：直线y=ax+b与圆x2+y2=1相交，则p 是q的（ ）
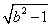；命题q：直线y=ax+b与圆x2+y2=1相交，则p是q的