题目内容
如果对于任意一个三角形,只要它的三边长a,b,c都在函数f(x)的定义域内,则 f(a),f(b),f(c)也是某个三角形的三边长,则称函数f(x)为“保三角形函数”.现有下列五个函数:
①f(x)=2x;
②f(x)=ex;
③f(x)=x2;
④f(x)=
;
⑤f(x)=sinx.
则其中是“保三角形函数”的有
①f(x)=2x;
②f(x)=ex;
③f(x)=x2;
④f(x)=
| x |
⑤f(x)=sinx.
则其中是“保三角形函数”的有
①④
①④
.(写出所有正确的序号)分析:欲判断函数f(x)是不是“保三角形函数”,只须任给三角形,设它的三边长a、b、c满足a+b>c,判断f(a)、f(b)、f(c)是否满足任意两数之和大于第三个数,即任意两边之和大于第三边即可.因此假设a≤c且b≤c,在各个选项中根据定义和函数对应法则加以判断,即可得到只有①④是“保三角形函数”,而其它的都可举出反例推翻.
解答:解:任给三角形,设它的三边长分别为a,b,c,则a+b>c,不妨假设a≤c,b≤c,
对于①,f(x)=2x,由于f(a)+f(b)=2(a+b)>2c=f(c),所以f(x)=2x是“保三角形函数”.
对于②,f(x)=ex,设a=b=2,c=3,a、b、c能构成三角形的三边
因为f(a)=f(b)=e2,f(c)=e3,而f(a)+f(b)=2e2<e3=f(c)
所以f(a)、f(b)、f(c)不能构成三角形的三边,故f(x)=ex不是“保三角形函数”.
对于③,f(x)=x2,3,3,5可作为一个三角形的三边长,但32+32<52,
不存在三角形以32,32,52为三边长,故f(x)=x2不是“保三角形函数”.
对于④,f(x)=
,由a+b>c,可得a+2
+b>c
两边开方得
+
>
,因此函数f(x)=
是“保三角形函数”.
对于⑤,对于f(x)=sinx,记a=2π,b=3π,c=5π,
则f(a)=f(b)=f(c)=0,不满足f(a)+f(b)>f(c)
所以f(x)=sinx,不是“保三角形函数”.
故答案为:①④
对于①,f(x)=2x,由于f(a)+f(b)=2(a+b)>2c=f(c),所以f(x)=2x是“保三角形函数”.
对于②,f(x)=ex,设a=b=2,c=3,a、b、c能构成三角形的三边
因为f(a)=f(b)=e2,f(c)=e3,而f(a)+f(b)=2e2<e3=f(c)
所以f(a)、f(b)、f(c)不能构成三角形的三边,故f(x)=ex不是“保三角形函数”.
对于③,f(x)=x2,3,3,5可作为一个三角形的三边长,但32+32<52,
不存在三角形以32,32,52为三边长,故f(x)=x2不是“保三角形函数”.
对于④,f(x)=
| x |
| ab |
两边开方得
| a |
| b |
| c |
| x |
对于⑤,对于f(x)=sinx,记a=2π,b=3π,c=5π,
则f(a)=f(b)=f(c)=0,不满足f(a)+f(b)>f(c)
所以f(x)=sinx,不是“保三角形函数”.
故答案为:①④
点评:本题给出新定义,要我们判定符合定义的函数个数.着重考查了函数的图象与性质、三角形的性质等知识,属于中档题.解题时需注意要判断f(x)为“保三角形函数”,要经过严密的论证说明f(x)满足“保三角形函数”的概念,但要判断f(x)不为“保三角形函数”,仅须要举出一个反例即可.

练习册系列答案
相关题目
 都在函数
都在函数 的定义域内,则
的定义域内,则 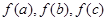 也是某个三角形的三边长,则称函数
也是某个三角形的三边长,则称函数 ;②
;② ;③
;③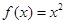 ;④
;④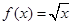 ;⑤
;⑤ .
. ;
;