题目内容
如图,已知圆O内接四边形ABCD中,AB=1,BC=2,CD=3,DA=4
求(1)四边形ABCD的面积;
(2)圆O的半径R.
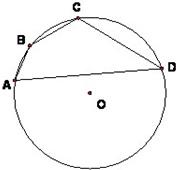
求(1)四边形ABCD的面积;
(2)圆O的半径R.

分析:(1)连接AC,在△ABC、△ACD中分别用由余弦定理求AC2,两式右边相等消去AC2,式子两角是互补的,得出角的正弦值,利用三角形面积公式可求出两个三角形的面积,加起来是要求的四边形的面积.
(2)由(1)可求出sin∠ADC和AC,利用正弦定理得直径,除以2得半径.
(2)由(1)可求出sin∠ADC和AC,利用正弦定理得直径,除以2得半径.
解答: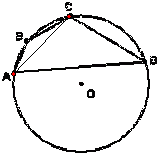 解:(1)连接AC,在△ABC中由余弦定理,得
解:(1)连接AC,在△ABC中由余弦定理,得
AC2=AB2+BC2-2AB•BCcos∠ABC=12+22-2×1×2cos∠ABC=5-4cos∠ABC(3分)
在△ACD中由余弦定理,得AC2=AD2+DC2-2AD•DCcos∠ADC=42+32-2×4×3cos∠ADC=25-24cos∠ADC(6分)
从而得5-4cos∠ABC=25-24cos∠ADC,
又∠ADC=π-∠ABC,故cos∠ADC=
,(9分)
sin∠ADC=
所以AC2=25-24×
=
.(10分)
所以S四边形ABCD=
(1×2+3×4)sin∠ADC=
×
=2
(12分)
(2)由2R=
=
×
,解得R=
(16分)
 解:(1)连接AC,在△ABC中由余弦定理,得
解:(1)连接AC,在△ABC中由余弦定理,得AC2=AB2+BC2-2AB•BCcos∠ABC=12+22-2×1×2cos∠ABC=5-4cos∠ABC(3分)
在△ACD中由余弦定理,得AC2=AD2+DC2-2AD•DCcos∠ADC=42+32-2×4×3cos∠ADC=25-24cos∠ADC(6分)
从而得5-4cos∠ABC=25-24cos∠ADC,
又∠ADC=π-∠ABC,故cos∠ADC=
| 5 |
| 7 |
sin∠ADC=
2
| ||
| 7 |
所以AC2=25-24×
| 5 |
| 7 |
| 55 |
| 7 |
所以S四边形ABCD=
| 1 |
| 2 |
| 14 |
| 2 |
2
| ||
| 7 |
| 6 |
(2)由2R=
| AC |
| sin∠ADC |
|
| 7 | ||
2
|
| ||
| 24 |
点评:本题两次用到余弦定理,衔接点有两处,一是有一条公共边,二是式子中两个角互补,圆内接四边形的对角补,要从图中读出,这点很重要;
正弦定理记忆的时候要全面,它的比值是三角形外接圆的直径,知道这一点,问题迎刃而解.
正弦定理记忆的时候要全面,它的比值是三角形外接圆的直径,知道这一点,问题迎刃而解.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,EC⊥平面ABC,AB=2AC=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,EC⊥平面ABC,AB=2AC=2,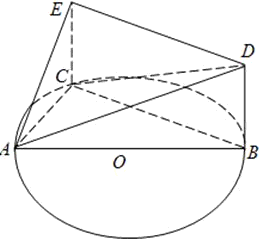 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,EC⊥平面ABC,AB=2AC=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,EC⊥平面ABC,AB=2AC=2, .
.