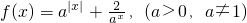题目内容
已知函数
(1)a>1,解关于x的方程f(x)=3.
(2)记函数g(x)=f(-x),x∈[-2,+∞),若g(x)的最值与a无关,求a的取值范围.
【答案】分析:(1)令 =3,对x的范围分类进行讨论求解即可.求解本题宜分为两类,分别为x≥0时与x<0时.
=3,对x的范围分类进行讨论求解即可.求解本题宜分为两类,分别为x≥0时与x<0时.
(2) 按a>1,与0<a<1分两类对函数的最值进行讨论,求出最值,若最值与参数无关,则此时的a的范围即所求.
解答:解:(1)令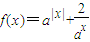 =3
=3
当x≥0时,方程变为a2x-3ax+2=0,解得ax=1或ax=2,可得=0或loga2
当x<0时,方程变为1+2=3ax,解得x=0故此类下无解.
综上 x=0或loga2(4分);
(2)由题设,g(x)=a|x|+2ax,x∈[-2,+∞),下分类讨论:
①若a>1,则
(ⅰ)当x≥0时,ax≥1,g(x)=3ax,∴g(x)∈[3,+∞)
(ⅱ)-2≤x<0时, ,g(x)=a-x+2ax
,g(x)=a-x+2ax
∴g'(x)=-a-xlna+2axlna=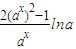
从而当 即
即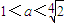 时,对?x∈(-2,0),g'(x)>0,
时,对?x∈(-2,0),g'(x)>0,
∴g(x)在[-2,0)上递增
∴g(x)∈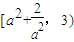 ,由此g(x)有最小值
,由此g(x)有最小值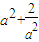 与a有关,不符合.
与a有关,不符合.
当 即
即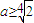 时,由g'(x)=0得
时,由g'(x)=0得
则 时,g'(x)<0;
时,g'(x)<0; 时,g'(x)>0
时,g'(x)>0
∴g(x)在 上递减,在
上递减,在 上递增,∴g(x)min=
上递增,∴g(x)min= =
=
g(x)有最小值为 与a无关,符合要求(6分)
与a无关,符合要求(6分)
②若0<a<1,则
(ⅰ)x≥0时,0<ax≤1,g(x)=3ax,∴g(x)∈(0,3]
(ⅱ)-2≤x<0时, ,g(x)=a-x+2ax,
,g(x)=a-x+2ax,
∴g'(x)=-a-xlna+2axlna= <0,∴g(x)在[-2,0)上递减,
<0,∴g(x)在[-2,0)上递减,
∴g(x)∈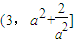 ,由此g(x)有最大值
,由此g(x)有最大值 与a有关,不符合
与a有关,不符合
综上:实数a的取值范围是 (6分).
(6分).
点评:本题的考点是指数函数的综合题,考查解指数方程与指数函数下的恒成立问题求参数,在第二小题的求解中,由于参数a的取值范围不同,转化的结果不同,故采取了分类讨论的方式来探究本题,此题难度较大,是训练复杂逻辑推理的一道好题,很好地训练了分类讨论的思想与转化化归的思想.
 =3,对x的范围分类进行讨论求解即可.求解本题宜分为两类,分别为x≥0时与x<0时.
=3,对x的范围分类进行讨论求解即可.求解本题宜分为两类,分别为x≥0时与x<0时.(2) 按a>1,与0<a<1分两类对函数的最值进行讨论,求出最值,若最值与参数无关,则此时的a的范围即所求.
解答:解:(1)令
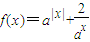 =3
=3当x≥0时,方程变为a2x-3ax+2=0,解得ax=1或ax=2,可得=0或loga2
当x<0时,方程变为1+2=3ax,解得x=0故此类下无解.
综上 x=0或loga2(4分);
(2)由题设,g(x)=a|x|+2ax,x∈[-2,+∞),下分类讨论:
①若a>1,则
(ⅰ)当x≥0时,ax≥1,g(x)=3ax,∴g(x)∈[3,+∞)
(ⅱ)-2≤x<0时,
 ,g(x)=a-x+2ax
,g(x)=a-x+2ax∴g'(x)=-a-xlna+2axlna=
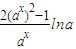
从而当
 即
即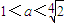 时,对?x∈(-2,0),g'(x)>0,
时,对?x∈(-2,0),g'(x)>0,∴g(x)在[-2,0)上递增
∴g(x)∈
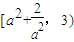 ,由此g(x)有最小值
,由此g(x)有最小值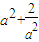 与a有关,不符合.
与a有关,不符合.当
 即
即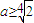 时,由g'(x)=0得
时,由g'(x)=0得
则
 时,g'(x)<0;
时,g'(x)<0; 时,g'(x)>0
时,g'(x)>0∴g(x)在
 上递减,在
上递减,在 上递增,∴g(x)min=
上递增,∴g(x)min= =
=
g(x)有最小值为
 与a无关,符合要求(6分)
与a无关,符合要求(6分)②若0<a<1,则
(ⅰ)x≥0时,0<ax≤1,g(x)=3ax,∴g(x)∈(0,3]
(ⅱ)-2≤x<0时,
 ,g(x)=a-x+2ax,
,g(x)=a-x+2ax,∴g'(x)=-a-xlna+2axlna=
 <0,∴g(x)在[-2,0)上递减,
<0,∴g(x)在[-2,0)上递减,∴g(x)∈
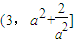 ,由此g(x)有最大值
,由此g(x)有最大值 与a有关,不符合
与a有关,不符合综上:实数a的取值范围是
 (6分).
(6分).点评:本题的考点是指数函数的综合题,考查解指数方程与指数函数下的恒成立问题求参数,在第二小题的求解中,由于参数a的取值范围不同,转化的结果不同,故采取了分类讨论的方式来探究本题,此题难度较大,是训练复杂逻辑推理的一道好题,很好地训练了分类讨论的思想与转化化归的思想.

练习册系列答案
相关题目