题目内容
已知函数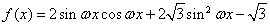 (
(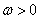 )的最小正周期为
)的最小正周期为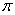 .
.
(1)求函数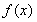 的单调增区间;
的单调增区间;
(2)将函数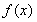 的图象向左平移
的图象向左平移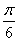 个单位,再向上平移
个单位,再向上平移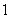 个单位,得到函数
个单位,得到函数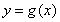 的图象.若
的图象.若 在
在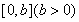 上至少含有
上至少含有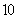 个零点,求
个零点,求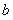 的最小值.
的最小值.
【答案】
(1)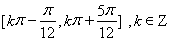 (2)
(2)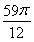
【解析】
试题分析:
(1)要求单调区间,首先要对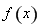 进行化简得到最间形式,依次利用正弦二倍角,降幂公式,和辅助角公式就可以得到
进行化简得到最间形式,依次利用正弦二倍角,降幂公式,和辅助角公式就可以得到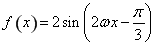 ,进而利用复合函数的单调性内外结合求得函数
,进而利用复合函数的单调性内外结合求得函数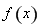 的单调区间.
的单调区间.
(2)利用“左加右减,上加下减”得到平移后的函数解析式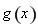 ,令
,令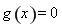 ,求出所有的零点,在根据
,求出所有的零点,在根据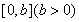 上至少含有
上至少含有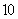 个零点,得到b的取值范围,进而得到b的最小值.
个零点,得到b的取值范围,进而得到b的最小值.
试题解析:
(1)由题意得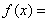
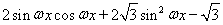
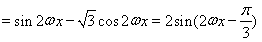 2分
2分
由周期为 ,得
,得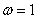 .得
.得 4分
4分
由正弦函数的单调增区间得 ,得
,得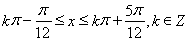
所以函数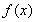 的单调增区间是
的单调增区间是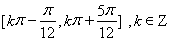 6分
6分
(2)将函数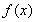 的图象向左平移
的图象向左平移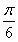 个单位,再向上平移1个单位,
个单位,再向上平移1个单位,
得到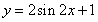 的图象,所以
的图象,所以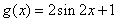 8分
8分
令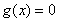 ,得:
,得: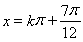 或
或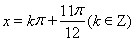 10分
10分
所以在每个周期上恰好有两个零点,若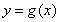 在
在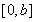 上有
上有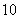 个零点,
个零点,
则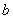 不小于第
不小于第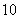 个零点的横坐标即可,即
个零点的横坐标即可,即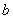 的最小值为
的最小值为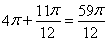 12分
12分
考点:零点 单调性 辅助角公式 正余弦倍角公式

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
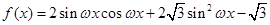 (
(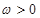 )的最小正周期为
)的最小正周期为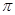 .
.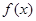 的单调增区间;
的单调增区间;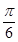 个单位,再向上平移
个单位,再向上平移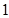 个单位,得到函数
个单位,得到函数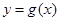 的图象.求
的图象.求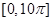 上零点的个数.
上零点的个数.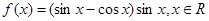 ,则
,则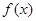 的最小正周期是 。
的最小正周期是 。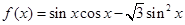 .
.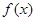 的最小正周期;
(II)求
的最小正周期;
(II)求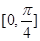 上的取值范围.
上的取值范围.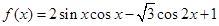 (
(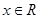 ).
).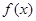 的最小正周期;
的最小正周期;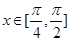 上的最大值和最小值;
上的最大值和最小值;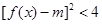 对任意
对任意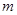 的取值范围.
的取值范围.