题目内容

设向量a=(sin x,sin x),b=(cos x,sin x),x∈.

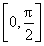(1)若|a|=|b|,求x的值;

(2)设函数f(x)=a·b,求f(x)的最大值.

 

【答案】

(1) x=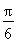 (2)

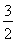
【解析】

解:(1)由|a|=|b|得=,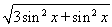

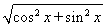即4sin2x=1.

又因为sin2x+cos2x=1,x∈.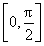

所以sin x=,x=.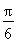

(2)f(x)=a·b=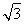sin xcos x+sin 2x,x∈.

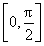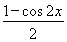f(x)=sin 2x+=sin 2x-cos 2x+=sin(2x-)+.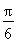

又2x-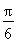∈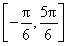,f(x)∈.

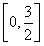即f(x)最大值为.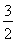

 

练习册系列答案
相关题目
设向量
a
=(sinα，1-cosα)，
b
=(sinβ，1+cosβ)，
c
=(0，1)，角α∈（0，π），β∈（π，2π），若
a
与
c
的夹角为θ1，
b
与
c
的夹角为θ2，且θ1-θ2=
π
3
，求tan（α-β）的值．
（2012•安徽模拟）已知函数f（x）=x2-mx在[1，+∞）上是单调函数．
（1）求实数m的取值范围；
（2）设向量
a
=(-sinα，2)，
b
=(-2sinα，
1
2
)，
c
=(cos2α，1)，
d
=(1，3)，求满足不等式f(
a
•
b
)＞f(
c
•
d
)的α的取值范围．
设向量a=(sinα，
3
2
)，b=(cosα，
1
2
)，且
a
∥
b
，则
a
的一个值为（　　）
A、
π
6
B、
π
4
C、
π
3
D、
5π
12
设向量
a
=(sin(x-
π
3
)，cos(x-
π
3
))，
b
=(cos(φ+
5π
6
)，sin(φ+
5π
6
))，若函数f（x）=
a
•
b
（0＜φ＜
π
2
）在x=-
π
3
处取得最大值．
（1）求函数f（x）在[0，π]上的单调递增区间；
（2）已知A为△ABC的内角，若f(A)=
1
4
，求f(
A+?
2
)的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网