题目内容
(本题满分14分)设函数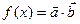 ,其中向量
,其中向量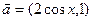 ,
,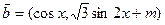
(1)求函数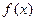 的最小正周期和单调递增区间
的最小正周期和单调递增区间
(2)当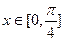 时,
时,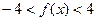 恒成立,求实数
恒成立,求实数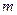 的取值范围
的取值范围
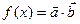 ,其中向量
,其中向量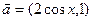 ,
,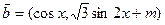
(1)求函数
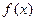 的最小正周期和单调递增区间
的最小正周期和单调递增区间(2)当
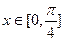 时,
时,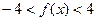 恒成立,求实数
恒成立,求实数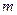 的取值范围
的取值范围依题意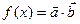 又
又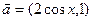 ,
,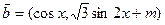
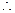
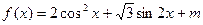
=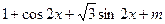 =
=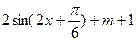 ……4分
……4分
设函数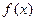 的最小正周期为T,则T=
的最小正周期为T,则T=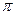 ……1分
……1分
当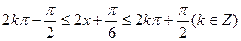 时,函数单调递增故解得
时,函数单调递增故解得
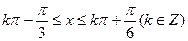
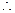 函数的单调递增区间为[
函数的单调递增区间为[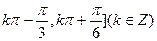 ……3分
……3分
(2)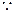
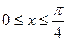
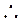
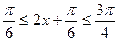
故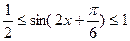
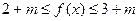
 3分
3分
依题意 当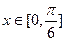 时,
时,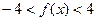 恒成立
恒成立
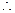
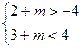 解得
解得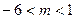
 3分
3分
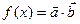 又
又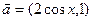 ,
,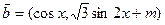
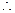
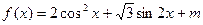
=
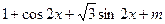 =
=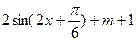 ……4分
……4分设函数
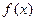 的最小正周期为T,则T=
的最小正周期为T,则T=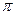 ……1分
……1分当
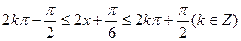 时,函数单调递增故解得
时,函数单调递增故解得 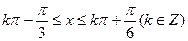
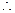 函数的单调递增区间为[
函数的单调递增区间为[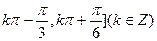 ……3分
……3分(2)
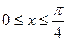
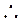
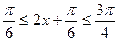
故
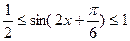
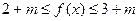
 3分
3分依题意 当
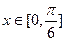 时,
时,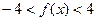 恒成立
恒成立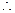
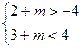 解得
解得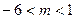
 3分
3分
练习册系列答案
相关题目
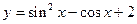 的最值。
的最值。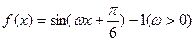 的导数
的导数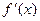 的最大值为3,则
的最大值为3,则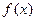 的图像的一条对称轴的方程是 ( )
的图像的一条对称轴的方程是 ( )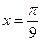
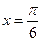
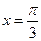
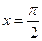
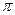 为周期,图象关于直线
为周期,图象关于直线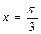 对称的函数是( )
对称的函数是( )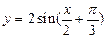

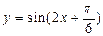

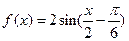 的最小正周期是
的最小正周期是 
 4
4
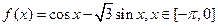 的单调递增区间是
的单调递增区间是



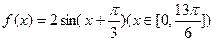 的图象与直线y=m的三个交点的横坐标分别为
的图象与直线y=m的三个交点的横坐标分别为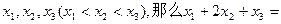 .
.