题目内容
已知函数
，其中n=
若函数f（x）在定义域内有零点，则a的取值范围是 ．
【答案】分析：先利用微积分基本定理求出n，得到函数的解析式，再求导函数，从而可确定函数的最小值，要使函数f（x）在定义域内有零点，则需最小值小于等于0即可．
解答：解：n=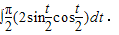
∴n=∫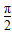
sintdt=-cost|
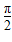=1，
从而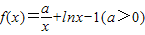
，
函数的定义域为（0，+∞）
∴
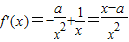
令f′（x）=0，∴x=a
当x∈（0，a）时，f′（x）＜0，当x∈（a，+∞）时，f′（x）＞0，
∴x=a时，函数f（x）取得最小值lna
∵函数f（x）在定义域内有零点
∴lna≤0
∴0＜a≤1
∴函数f（x）在定义域内有零点时，a的取值范围是（0，1]
故答案为：（0，1]．
点评：本题以函数为载体，考查微积分基本定理，导数的运用，考查函数的零点，解题的关键是将函数f（x）在定义域内有零点，转化为最小值小于等于0．本题属于基础题．
解答：解：n=
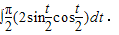
∴n=∫
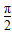sintdt=-cost|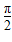=1，从而
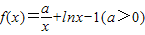，函数的定义域为（0，+∞）
∴
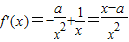
令f′（x）=0，∴x=a
当x∈（0，a）时，f′（x）＜0，当x∈（a，+∞）时，f′（x）＞0，
∴x=a时，函数f（x）取得最小值lna
∵函数f（x）在定义域内有零点
∴lna≤0
∴0＜a≤1
∴函数f（x）在定义域内有零点时，a的取值范围是（0，1]
故答案为：（0，1]．
点评：本题以函数为载体，考查微积分基本定理，导数的运用，考查函数的零点，解题的关键是将函数f（x）在定义域内有零点，转化为最小值小于等于0．本题属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
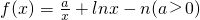，其中n=
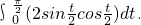若函数f（x）在定义域内有零点，则a的取值范围是________．
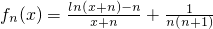（其中n为常数，n∈N*），将函数fn（x）的最大值记为an，由an构成的数列{an}的前n项和记为Sn．
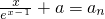，求a的取值范围；
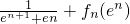与an的大小，并加以证明．
，其中n∈N*，a为常数．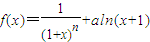
，其中n∈N*，a为常数．