题目内容

,4,6
 
(本小题满分12分) 已知定义域为R的函数是奇函数．

(1) 求的值；

(2)若对任意的, 不等式恒成立, 求k的取值范围.

(1) 的值依次是2、1，(2)


解析:

(1)因为是奇函数, 所以=0, 即

又由知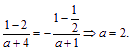

(2) 解法一：由(1)知, 易知在上为减函

数。又因是奇函数，从而不等式：等价于

.因为减函数,由上式推得:．

即对一切有：, 从而判别式

解法二：由(1)知．又由题设条件得：

　　　　　　　　　

即：  

整理得:    .上式对一切均成立, 从而判别式

练习册系列答案
相关题目
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据：
x 3 4 5 6
y 2.5 3 4 4.5
（1）请画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；
（3）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？
（参考公式：
b
=
n
i=1
xiyi-n
.
xy
n
i=1
xi2-n
.
x
2
，
a
=
.
y
-b
.
x
；参考数值：3×2.5+4×3+5×4+6×4.5=66.5）
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
A．（不等式选做题）不等式|x-5|+|x+3|≥10的解集是
（-∞，-4]∪[6，+∞）
（-∞，-4]∪[6，+∞）
．
B．（坐标系与参数方程选做题）在极坐标系中，圆ρ=-2sinθ的圆心的极坐标是
（1，
3π
2
）
（1，
3π
2
）
．
C．（几何证明选做题）如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=2
2
，BE=1，BF=2，若CE与圆相切，则线段CE的长为
7
7
．
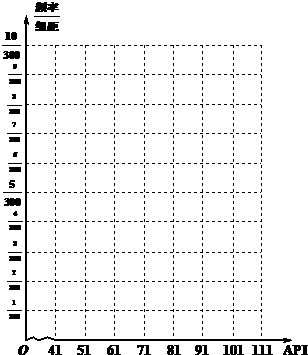城市的空气质量以其空气质量指数API（为整数）衡量，指数越大，级别越高，说明污染越严重，对人体健康的影响也越明显．根据空气质量指数API的不同，可将空气质量分级如下表：
API 0～50 51～100 101～150 151～200 201～250 251～300 ＞300
状况 优 良 轻微污染 轻度污染 中度污染 中度重污染 重度污染
为了了解某城市2011年的空气质量情况，现从该城市一年空气质量指数API的监测数据库中，用简单随机抽样方法抽取30个空气质量指数API进行分析，得到如下数据：
API分组 [41，51） [51，61） [61，71） [71，81） [81，91） [91，101） [101，111]
频数   2     1    4    6   10 5   2
（Ⅰ）完成下面频率分布直方图，并求质量指数API的中位数大小；
（Ⅱ）估计该城市一年中空气质量为优良的概率；
（Ⅲ）请你依据所给数据和上述分级标准，对该城市的空气质量给出一个简短评价．
（2013•蓟县二模）某工厂生产的零件标准分成9个等级，等级系数X依次为1，2，…，9，X≥4为合格标准，且该厂的零件都符合相应的合格标准．从该厂生产的零件中随机抽取30件，相应的等级系数组成一个样本，数据如下：
4   6   4   4   9   6   6   7   4   5
7   4   5   8   6   4   5   9   6   4
9   4   5   4   5   5   8   6   7   8
规定零件的等级系数X≥8的为一等品，等级系数6≤X＜8的为二等品，等级系数4≤X＜6的为三等品．
（Ⅰ）试分别估计该厂生产的零件一等品频率、二等品频率和三等品频率；
（Ⅱ）从样本的一等品中随机抽取2件，
①列出两件产品等级系数的所有结果；
②求所抽得2件产品等级系数不同的概率．
为了参加广州亚运会，从四支较强的排球队中选出18人组成女子排球国家队，队员来源人数如下表：
队别 北京 上海 天津 八一
人数 4 6 3 5
（Ⅰ）从这18名队员中随机选出两名，求两人来自同一支队的概率；
（Ⅱ）中国女排奋力拼搏，战胜韩国队获得冠军．若要求选出两位队员代表发言，求这两名队员至多一名来自北京队的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网