题目内容
设O是平面ABC外一点,点M满足条件
=
+
+
,则直线AM( )
| OM |
| 3 |
| 4 |
| OA |
| 1 |
| 8 |
| OB |
| 1 |
| 8 |
| OC |
分析:根据题中向量等式,将向量
进行拆分,移项整理可得
=-
-
,从而得到向量
、
、
是共面向量,由此不难得到本题答案.
| OM |
| MA |
| 1 |
| 6 |
| MB |
| 1 |
| 6 |
| MC |
| MA |
| MB |
| MC |
解答:解:∵
=
+
+
∴由
=
+
+
,得
+
+
=
+
+
移项,得
(
-
)=
(
-
)+
(
-
)
∴
=
+
,即
=-
-
由此可得向量
、
、
是共面向量,由此可得直线AM在平面ABC内
故选:D
| OM |
| 3 |
| 4 |
| OM |
| 1 |
| 8 |
| OM |
| 1 |
| 8 |
| OM |
∴由
| OM |
| 3 |
| 4 |
| OA |
| 1 |
| 8 |
| OB |
| 1 |
| 8 |
| OC |
| 3 |
| 4 |
| OM |
| 1 |
| 8 |
| OM |
| 1 |
| 8 |
| OM |
| 3 |
| 4 |
| OA |
| 1 |
| 8 |
| OB |
| 1 |
| 8 |
| OC |
移项,得
| 3 |
| 4 |
| OM |
| OA |
| 1 |
| 8 |
| OB |
| OM |
| 1 |
| 8 |
| OC |
| OM |
∴
| 3 |
| 4 |
| AM |
| 1 |
| 8 |
| MB |
| 1 |
| 8 |
| MC |
| MA |
| 1 |
| 6 |
| MB |
| 1 |
| 6 |
| MC |
由此可得向量
| MA |
| MB |
| MC |
故选:D
点评:本题给出向量等式,求证点M是平面ABC内的点,着重考查了平面向量的减法法则和平面向量基本定理及其应用等知识,属于基础题.

练习册系列答案
相关题目
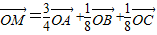 ,则直线AM( )
,则直线AM( )