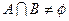题目内容
设集合A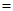 {a, b},则满足A∪B
{a, b},则满足A∪B 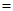 {a, b, c, d}的集合B的子集最多个数是( )
{a, b, c, d}的集合B的子集最多个数是( )
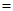 {a, b},则满足A∪B
{a, b},则满足A∪B 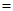 {a, b, c, d}的集合B的子集最多个数是( )
{a, b, c, d}的集合B的子集最多个数是( )| A.4 | B.8 | C.16 | D.32 |
C
根据A∪B={a,b,c,d},得到集合B含有元素最多的情形,求出集合B子,根据子集的含义知,集合B的子集中的元素是从集合B中取得,对于每一个元素都有取或不取两种方法,同乘法原理即可其子集的个数.
解:由A∪B={a,b,c,d},得到集合B含有元素最多的情形是:B={a,b,c,d},
∵含有n个元素的集合的子集共有:2n个,
∴集合B={a,b,c,d},的子集个数24=16.
故选C.
解:由A∪B={a,b,c,d},得到集合B含有元素最多的情形是:B={a,b,c,d},
∵含有n个元素的集合的子集共有:2n个,
∴集合B={a,b,c,d},的子集个数24=16.
故选C.

练习册系列答案
相关题目
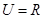 ,集合
,集合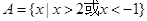 ,
,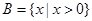 ,则
,则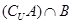 等于
等于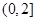
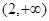
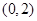
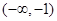

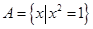 ,
,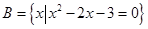 ,则
,则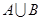 = ( )
= ( )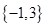

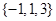
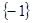
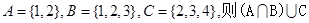 ( )
( )
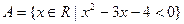 ,Z为整数集,则集合
,Z为整数集,则集合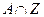 中所有元素的和等于________
中所有元素的和等于________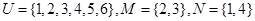 ,则集合
,则集合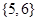 等于( )
等于( )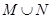
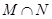
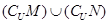

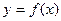 的定义域与值域都是R,且单调递增,
的定义域与值域都是R,且单调递增,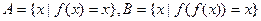 ,则
,则  .
. 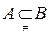 B.
B. 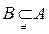 C. A=B D.
C. A=B D.