题目内容
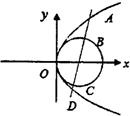78、如图，过抛物线y2=4x的焦点F的直线交抛物线与圆（x-1）2+y2=1于A，B，C，D四点，则|AB|•|CD|=1
．分析：当直线过焦点F且垂直于x轴时，|AD|=2p=4，|BC|=2r=2，由抛物线与圆的对称性知：|AB|=|CD|=1，所以|AB|•|CD|=1．
解答：解：由特殊化原则，
当直线过焦点F且垂直于x轴时，
|AD|=2p=4，
|BC|=2r=2，
由抛物线与圆的对称性知：
|AB|=|CD|=1，
所以|AB|•|CD|=1；
故答案为1．
当直线过焦点F且垂直于x轴时，
|AD|=2p=4，
|BC|=2r=2，
由抛物线与圆的对称性知：
|AB|=|CD|=1，
所以|AB|•|CD|=1；
故答案为1．
点评：本题考查圆的性质和应用，解题时恰当地选取取特殊值，能够有效地简化运算．
练习册系列答案
相关题目
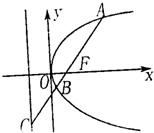如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为
如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B（|AF|＞|BF|），交其准线于点C，若|BC|=2|BF|，且|AF|=2，则此抛物线的方程为
如图，过抛物线y2=2px（p＞0）的焦点F且倾斜角为60°的直线l交抛物线于A、B两点，若|AF|=3，则此抛物线方程为（ ）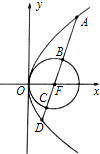
如图，过抛物线y2=4x焦点的直线依次交抛物线与圆（x-1）2+y2=1于A，B，C，D，则