题目内容
若全集U＝{1，2，3，4，5，6}，M∩N＝N，N＝{1，4}，试求满足条件的集合M的个数．
16
由M∩N＝N得M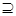
N.
含有2个元素的集合M有1个，含有3个元素的集合M有4个，含有4个元素的集合M有6个，含有5个元素的集合M有4个，含有6个元素的集合M有1个．
因此，满足条件的集合M有1＋4＋6＋4＋1＝16个．
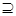N.含有2个元素的集合M有1个，含有3个元素的集合M有4个，含有4个元素的集合M有6个，含有5个元素的集合M有4个，含有6个元素的集合M有1个．
因此，满足条件的集合M有1＋4＋6＋4＋1＝16个．
练习册系列答案
相关题目
，集合B＝{a2，a＋b，0}，若A＝B，求a2 013＋b2 014的值．
},B={a},若B⊆A,则实数a的值为 .
则
( )
, 集合
, 则
，集合
，
，则
( )
