题目内容
对于任意正整数n,定义“n的双阶乘n!!”如下:
当n是偶数时,n!!=n·(n-2)·(n-4)……6·4·2;
当n是奇数时,n!!=n·(n-2)·(n-4)……5·3·1
现在有如下四个命题:①(2003!!)·(2002!!)=2003!;②2002!!=21001·1001!;
③2002!!的个位数是0; ④2003!!的个位数是5.
其中正确的命题有( )
当n是偶数时,n!!=n·(n-2)·(n-4)……6·4·2;
当n是奇数时,n!!=n·(n-2)·(n-4)……5·3·1
现在有如下四个命题:①(2003!!)·(2002!!)=2003!;②2002!!=21001·1001!;
③2002!!的个位数是0; ④2003!!的个位数是5.
其中正确的命题有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
A
解:因为当n是偶数时,n!!=n·(n-2)·(n-4)……6·4·2;
当n是奇数时,n!!=n·(n-2)·(n-4)……5·3·1
①(2003!!)·(2002!!)=2003!;②2002!!=21001·1001!;
③2002!!的个位数是0; ④2003!!的个位数是5.
炎症可知都满足公式成立。选A
当n是奇数时,n!!=n·(n-2)·(n-4)……5·3·1
①(2003!!)·(2002!!)=2003!;②2002!!=21001·1001!;
③2002!!的个位数是0; ④2003!!的个位数是5.
炎症可知都满足公式成立。选A

练习册系列答案
相关题目
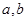 为实数,则“
为实数,则“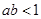 ”是“
”是“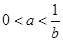 ”的( )
”的( )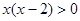 ”是“不等式
”是“不等式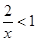 ”成立的 ( )
”成立的 ( ) 都是实数,则“
都是实数,则“ ”是“
”是“ ”的( )
”的( )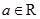 ,则“
,则“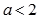 ”是“
”是“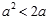 ”的 ( )
”的 ( )  成立的充分不必要条件是( )
成立的充分不必要条件是( )



 ;
;  ;
; ”是“
”是“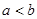 ”的必要不充分条件;
”的必要不充分条件; 是幂函数,且在(0,+
是幂函数,且在(0,+ )上递减.
)上递减.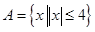 ,
,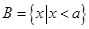 ,则“
,则“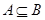 ”是“
”是“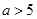 ”的( )
”的( )