题目内容
19.已知f(x)是定义在R上的函数,且满足f(-x)=f(x),f(x+2)=f(2-x).若曲线y=f(x)在x=-1处的切线方程为x-y+3=0,则该曲线在x=5处的切线方程为( )| A. | x-y-3=0 | B. | x-y-7=0 | C. | x+y-3=0 | D. | x+y-7=0 |
分析 由f(-x)=f(x),f(x+2)=f(2-x),可令x为x+2,可得f(x)为周期为4的函数,再由x=-1处的切线方程为x-y+3=0,可得f(1),f(5),再通过求导,可得导函数为奇函数且为周期函数,即可求得f′(5),由点斜式方程,即可得到所求切线方程.
解答 解:由f(-x)=f(x),f(x+2)=f(2-x),
即有f(x+4)=f(2-(x+2))=f(-x)=f(x),
则f(x)为周期为4的函数,
若曲线y=f(x)在x=-1处的切线方程为x-y+3=0,
则f(-1)=2,f′(-1)=1,
即有f(5)=f(1)=f(-1)=2,
对f(-x)=f(x),两边求导,可得-f′(-x)=f′(x),
由f(x+4)=f(x),可得f′(x+4)=f′(x),
即有f′(5)=f′(1)=-f′(-1)=-1,
则该曲线在x=5处的切线方程为y-2=-(x-5),
即为x+y-7=0.
故选:D.
点评 本题考查导数的运用:求切线方程,主要考查导数的几何意义,同时考查函数的奇偶性和周期性的运用,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
11.记函数f(x)的导函数为f′(x),若f(x)对应的曲线在点(x0,f(x0))处的切线方程为y=-x+1,则( )
| A. | f′(x0)=2 | B. | f′(x0)=1 | C. | f′(x0)=0 | D. | f′(x0)=-1 |
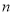 的值是( )
的值是( )
 ,
,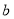 ,
,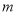 是正数,求证:
是正数,求证: .
. 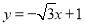 的大致图象,则直线
的大致图象,则直线 轴夹角
轴夹角 大小为( )
大小为( )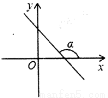
 B.
B.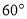
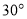 D.
D.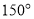
 满足
满足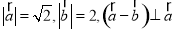 ,则
,则 与
与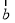 的夹角是( )
的夹角是( ) B.
B.
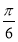 D.
D.