题目内容
集合A={(x,y)|x2+y2=4},B={(x,y)|(x-3)2+(y-4)2=r2},其中r>0,若A∩B中有且仅有一个元素,则r的值是______________.
【答案】
3或7
【解析】本题主要考查两圆的位置关系和基本的运算技能,
已知⊙O1(x-a)2+(y-b)2= ,⊙O2(x-c)2+(y-d)2=
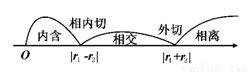
,⊙O2(x-c)2+(y-d)2=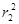 ,其中r1>0,r2>0,①当|O1O2|=|r1-r2|时,⊙O1与⊙O2相内切,②当|O1O2|=|r1+r2|时,⊙O1与⊙O2相外切,③当0≤|O1O2|<|r1-r2|时两圆内含,④当|r1-r2|<|O1O2|<|r1+r2|时,两圆相交,⑤当|O1O2|>r1+r2时两圆相离.
,其中r1>0,r2>0,①当|O1O2|=|r1-r2|时,⊙O1与⊙O2相内切,②当|O1O2|=|r1+r2|时,⊙O1与⊙O2相外切,③当0≤|O1O2|<|r1-r2|时两圆内含,④当|r1-r2|<|O1O2|<|r1+r2|时,两圆相交,⑤当|O1O2|>r1+r2时两圆相离.
本题中A∩B只有一个元素,∴两圆相内切或外切,∴|O1O2|=|r1±r2|.当两圆外切时,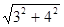 =2+r,r=3,两圆内切时,
=2+r,r=3,两圆内切时,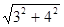 =r-2,r=7,所以r的值是3或7.
=r-2,r=7,所以r的值是3或7.

练习册系列答案
相关题目

 },集合B={(x,y)
},集合B={(x,y)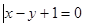 ,且0
,且0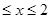 },又A
},又A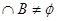 ,求实数m的取值范围
,求实数m的取值范围