题目内容
给出以下结论:
①甲从四面体中任意选择一条棱,乙也从该四面体中任意选择一条棱,则所得的两条棱所在的直线是异面直线的概率是
;
②等比数列{an}中,若a3=2,a7=8,则a5=±4.
③若关于x的方程x-
+k=0在x∈(0,1)上没有实数根,则k的取值范围是k≥2;
④在△ABC中,若sinA>sinB,则cosA<cosB;
其中正确的结论是
①甲从四面体中任意选择一条棱,乙也从该四面体中任意选择一条棱,则所得的两条棱所在的直线是异面直线的概率是
| 1 |
| 6 |
②等比数列{an}中,若a3=2,a7=8,则a5=±4.
③若关于x的方程x-
| 1 |
| x |
④在△ABC中,若sinA>sinB,则cosA<cosB;
其中正确的结论是
④
④
(填上所有正确结论的序号)分析:①先求出四面体棱中异面直线的对数,再利用古典概型求概率判断;
②利用等比数列的性质求解,判断②是否正确;
③利用导数判定函数的单调性,再求函数的值域,利用函数思想分析判断即可.
④根据在△中,sinA>sinB的充要条件是A>B,再利用余弦函数的单调性判断④是否正确.
②利用等比数列的性质求解,判断②是否正确;
③利用导数判定函数的单调性,再求函数的值域,利用函数思想分析判断即可.
④根据在△中,sinA>sinB的充要条件是A>B,再利用余弦函数的单调性判断④是否正确.
解答:解:①∵四面体两条棱所在直线共有3对异面直线
=
,∴①错误;
②根据等比数列的性质, a52=a3×a7=16,∴a5=±4,又∵a5=-4 时,a4不存在,∴a5=4∴②错误;
③∵t=
-x,t′=-
-1,x∈(0,1),t′(x)<0,∴t(x)在(0,1)上递减∴
-x∈(0,+∞),∵k=
-x,无实根,∴k≤0,故③错误;
④∵在△ABC中,sinA>sinB?A>B,又在(0,π)上y=cosx递减,∴cosA<cosB,∴④正确.
故答案是④
| 3 |
| 6×6 |
| 1 |
| 12 |
②根据等比数列的性质, a52=a3×a7=16,∴a5=±4,又∵a5=-4 时,a4不存在,∴a5=4∴②错误;
③∵t=
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
④∵在△ABC中,sinA>sinB?A>B,又在(0,π)上y=cosx递减,∴cosA<cosB,∴④正确.
故答案是④
点评:本题借助考查命题的真假判断,考查等比数列的性质、导数的应用及概率统计.

练习册系列答案
相关题目
 ;
;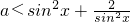 恒成立,则a的取值范围是
恒成立,则a的取值范围是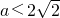 ;
; 上没有实数根,则k的取值范围是k≥2;
上没有实数根,则k的取值范围是k≥2; ;
; 恒成立,则a的取值范围是
恒成立,则a的取值范围是 ;
; 上没有实数根,则k的取值范围是k≥2;
上没有实数根,则k的取值范围是k≥2; ;
; 恒成立,则a的取值范围是
恒成立,则a的取值范围是 ;
; 上没有实数根,则k的取值范围是k≥2;
上没有实数根,则k的取值范围是k≥2;