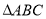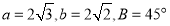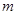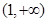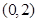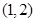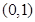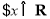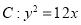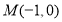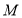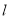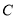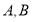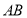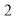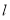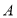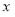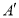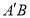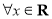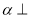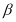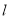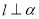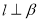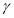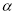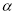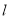题目内容
已知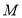 为椭圆
为椭圆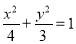 上一点,
上一点,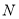 为椭圆长轴上一点,
为椭圆长轴上一点,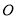 为坐标原点.
为坐标原点.
给出下列结论:
①存在点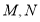 ,使得
,使得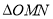 为等边三角形;
为等边三角形;
②不存在点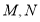 ,使得
,使得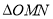 为等边三角形;
为等边三角形;
③存在点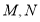 ,使得
,使得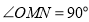 ;
;
④不存在点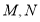 ,使得
,使得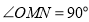 .
.
其中,所有正确结论的序号是__________.
①④
【解析】
试题分析:若过存在点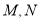 ,使得
,使得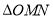 为等边三角形,由椭圆的对称性设
为等边三角形,由椭圆的对称性设 点在第一象限
点在第一象限 .代入椭圆方程可得
.代入椭圆方程可得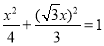 .解得
.解得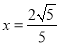 .所以
.所以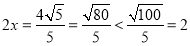 .所以存在点
.所以存在点 .所以①正确;若存在点
.所以①正确;若存在点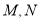 ,使得
,使得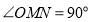 ,同样设
,同样设 ,代入椭圆方程可得
,代入椭圆方程可得 ,解得
,解得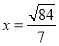 .所以
.所以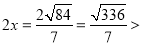
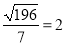 .所以不存在点
.所以不存在点 .所以④正确.故填①④.
.所以④正确.故填①④.
考点:1.直线与椭圆的位置关系.2.利用方程的思想解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目