题目内容

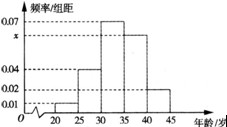精英家教网为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，其中年龄分组区间是：[20，25）、[25，30）、[30，35）、[35，40）、[40，45]．
（1）求图中x的值并根据频率分布直方图估计这500名志愿者中年龄在[35，40）的人数；
（2）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动，再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人．求抽取的3名志愿者中恰有2名年龄低于35岁的概率．
分析：（1）由直方图求出除[35，40）外的频率，得到在[35，40）内的频率，除以5得到x的值；
（2）求出用分层抽样方法抽取的20名中年龄低于35岁的人数及年龄不低于35岁的人数，利用简单的排列组合知识求出基本事件总数和恰有2名年龄低于35岁的事件数，然后由古典概型概率计算公式求解．
解答：解：（1）∵小矩形的面积等于频率，∴除[35，40）外的频率和为0.70．
∴x=
1-0.70
5
=0.06．
故在500名志愿者中，年龄在[35，40）岁的人数为0.06×5×500=150．
（2）用分层抽样的方法，从中选取20名，则其中“年龄低于35岁”的人有12名，“年龄不低于35岁”的人有8名．
∴抽取的3名志愿者中恰有2名年龄低于35岁的概率为
C
2
12
•
C
1
8
C
3
20
=
44
95
．
点评：本题考查了频率分布直方图，考查了古典概型及其概率计算公式，考查了简单的排列与组合知识，是基础的计算题．
练习册系列答案
相关题目
为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者，从符合条件的500名志愿者中随机抽样100名志原者的年龄情况如下表所示．
（Ⅰ）频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图（如图）再根据频率分布直方图估计这500名志愿者中年龄在[30，35）岁的人数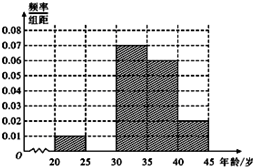；精英家教网
分组（单位：岁） 频数 频率
[20，25] 5 0.05
[25，30] ① 0.20
[30，35] 35 ②
[35，40] 30 0.30
[40，45] 10 0.10
合计 100 1.00
（Ⅱ）在抽出的100名志原者中按年龄再采用分层抽样法抽取20人参加中心广场的宣传活动，从这20人中选取2名志愿者担任主要负责人，记这2名志愿者中“年龄低于30岁”的人数为X，求X的分布列及数学期望．
为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者的年龄情况如下表所示．
（1）频率分布表中的①②位置应填什么数据？
（2）画出频率分布直方图；
（3）估计这500名志愿者中年龄在[30，35）岁的人数．
分组（单位：岁） 频数 频率
[20，25） 5 0.050
[25，30） ① 0.200
[30，35） 35 ②
[35，40） 30 0.300
[40，45） 10 0.100
合计 100 1.00
（2013•顺义区二模）为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，其中年龄分组区间是：[20，25），[25，30），[30，35），[35，40），[40，45]．
（I）求图中x的值并根据频率分布直方图估计这500名志愿者中年龄在[35，40）岁的人数；
（II）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动，再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人．记这3名志愿者中“年龄低于35岁”的人数为X，求X的分布列及数学期望．

为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:.

(I)求图中的值并根据频率分布直方图估计这500名志愿者中年龄在岁的人数;

(II)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为,求的分布列及数学期望.

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网