题目内容
将长为l的铁丝剪成两段,各围成长与宽之比为2∶1及3∶2的矩形,那么这两个矩形面积和的最小值为 .
【答案】
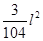
【解析】
试题分析:设剪成2段中其中一段为xcm,另一段为(l-x)cm,依题意知:
S=S1+S2=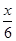 •
•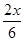 +
+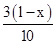 •
•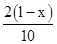 =
=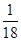 x2+
x2+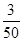 (l-x)2,
(l-x)2,
所以:S′=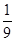 x-
x- (l-x),
(l-x),
令S′=0,则x=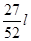 .另一段为
.另一段为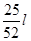 .
.
此时Smin=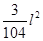
故答案为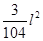 。
。
考点:本题主要考查导数的应用。
点评:理解题意,构建函数模型是关键,记牢公式,求导计算。因为此题是二次函数,所以极值点处就是最值点。

练习册系列答案
相关题目