题目内容
求过两直线3x+4y-2=0和2x+y+2=0的交点且与直线3x-2y+4=0垂直的直线方程.
【答案】分析:由已知中直线3x+4y-2=0和2x+y+2=0的方程,我们联立方程组,可以求出其交点坐标,进而根据所求直线于直线3x-2y+4=0垂直,设出直线方程,将交点坐标代入,即可得到所求直线的方程.
解答:解:设与直线3x-2y+4=0垂直的直线方程为2x+3y+a=0,(a∈R)…(3分)
由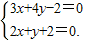 可以得到
可以得到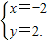 故交点的坐标为 (-2,2)…(6分)
故交点的坐标为 (-2,2)…(6分)
又由于交点在所求直线上,因此 2×(-2)+3×2+a=0,(a∈R)
从而a=-2…(9分)
故所求的直线方程为2x+3y-2=0.…(12分)
点评:本题考查的知识点是直线的一般式方程与直线的垂直关系,两条直线的交点坐标,其中根据两直线垂直时一般式方程的系数关系,设出所求直线的解析式,是解答本题的关键.
解答:解:设与直线3x-2y+4=0垂直的直线方程为2x+3y+a=0,(a∈R)…(3分)
由
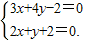 可以得到
可以得到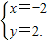 故交点的坐标为 (-2,2)…(6分)
故交点的坐标为 (-2,2)…(6分)又由于交点在所求直线上,因此 2×(-2)+3×2+a=0,(a∈R)
从而a=-2…(9分)
故所求的直线方程为2x+3y-2=0.…(12分)
点评:本题考查的知识点是直线的一般式方程与直线的垂直关系,两条直线的交点坐标,其中根据两直线垂直时一般式方程的系数关系,设出所求直线的解析式,是解答本题的关键.

练习册系列答案
相关题目