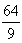题目内容

设A＝{x|－4＜x＜－}，B＝{x|x≤－4}，求A∪B，A∩B，（RA）∩（RB），R（A∪B）.?

解：A∪B＝{x|－4＜x＜－}∪{x|x≤－4}＝{x|x＜－},

A∩B＝{x|－4＜x＜－}∩{x|x≤－4}＝

(RA)∩(RB)={x|x≤－4或x≥－}∩{x|x>－4}={x|x≥－}.

*R(A∪B)={x|x≥－}.


练习册系列答案
相关题目

填空题

(1)若A，B不是空集，用适当的符号(，)填空：

A∩B________A，A∩B________B，A∪B________A，A∪B________B，

A∩B________A∪B；

(2)设A＝{x|x是锐角三角形}，B＝{x|x是钝角三角形}，则A∩B＝________；

(3)设A＝{x|x是平行四边形)，B＝{x|x是菱形}，则A∪B＝________；

(4)设A＝{(x，y)|2x－y＝1}，B＝{(x，y)|5x＋y＝6}，

C＝{(x，y)|2x＝y＋1|，D＝{(x，y)|2x－y＝8}，

则A∩B＝________，B∩C＝________，A∩D＝________；

(5)设A＝{x|－5＜x＜2}，B＝{x|－2＜x＜5}，则A∪B＝________；

(6)在直角坐标平面内，x轴上点的集合用描述法可表示为________；

在直角坐标平面内，不在第一、三象限的点的集合用描述法可表示为________．

设A＝{x|－4＜x＜2}，B＝{x|－m－1＜x＜m－1，m＞0}．求分别满足下列条件的m的取值集合：

(1)AB；

(2)A∩B≠．

设A＝{x|－4＜x＜3}，B＝{x|－m－1＜x＜m－1，m＞0}，若A∩B≠，求m的取值集合．
设a＝(x，4，3)，b＝(3，2，z)，且a∥b，则xz的值为(　　)

A.9                B.-9               C.4                D.Equation.3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网