题目内容
设样本(x1,x2,…,xm)的平均数为
,样本(y1,y2,…,yn)的平均数为
(
≠
),若样本(x1,x2,…,xm,y1,y2,…,yn)的平均数为
=
+
,则
=
. |
| x |
. |
| y |
. |
| x |
. |
| y |
. |
| z |
| 1 |
| 3 |
. |
| x |
| 2 |
| 3 |
. |
| y |
| n |
| m |
2
2
.分析:根据平均数的定义,写出两组变量之间的关系,把变化的数据整理,变成两组已知数据之间的关系,利用平均数的公式,代入数据求出结果.
解答:解:由平均数的定义知x1+x2+…+xm=m
,y1+y2+…+yn=n
,
∴样本(x1,x2,…,xm,y1,y2,…,yn)的平均数为:
(x1+x2+…+xm+y1+y2+…+yn)
=
(m
+n
),
因
=
+
,
∴
,
∴
=2
故答案为:2
. |
| x |
. |
| y |
∴样本(x1,x2,…,xm,y1,y2,…,yn)的平均数为:
| 1 |
| m+n |
=
| 1 |
| m+n |
. |
| x |
. |
| y |
因
. |
| z |
| 1 |
| 3 |
. |
| x |
| 2 |
| 3 |
. |
| y |
∴
|
∴
| n |
| m |
故答案为:2
点评:本题是求一组数据的平均数,解题过程容易出错,要记住下列原则不管是遇到求那组数据的平均数,做法都是一样的,求出所有数的和再除以数据个数.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 (2013•安徽)为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中为各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如下:
(2013•安徽)为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中为各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如下:
 ,样本(y1,y2,…,yn)的平均数为
,样本(y1,y2,…,yn)的平均数为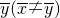 ,若样本(x1,x2,…,xm,y1,y2,…,yn)的平均数为
,若样本(x1,x2,…,xm,y1,y2,…,yn)的平均数为 =________.
=________.