题目内容
已知圆C：(x-2)2+y2=36，定点A(2,0)，若P是圆上的动点，AP的垂直平分线交CP于R，求R的轨迹方程.
解析：∵R是AP垂直平分线上的点，如图所示,∴|RP|=|RA|.
又|CR|+|RP|=|CP|=r=6,∴|CR|+|RA|=6.而6＞4=|CA|,
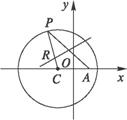
∴R点的轨迹是以C(-2,0)、A(2,0)为焦点，且长轴长为6的椭圆.
∴2a=6,a=3,c=2.
∴b=
.
∴点R的轨迹方程为
+
=1.
练习册系列答案
相关题目
题目内容
已知圆C：(x-2)2+y2=36，定点A(2,0)，若P是圆上的动点，AP的垂直平分线交CP于R，求R的轨迹方程.
解析：∵R是AP垂直平分线上的点，如图所示,∴|RP|=|RA|.
又|CR|+|RP|=|CP|=r=6,∴|CR|+|RA|=6.而6＞4=|CA|,
∴R点的轨迹是以C(-2,0)、A(2,0)为焦点，且长轴长为6的椭圆.
∴2a=6,a=3,c=2.
∴b=.
∴点R的轨迹方程为+=1.
)2＋(y－1)2＝4和直线l：x－y＝5，求C上的点到直线的距离的最大值与最小值．
的最大值是（ ）。