题目内容

设A、B、C、D是空间不共面的四点，且满足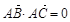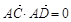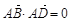，，，则△BCD是   （   ）

   （A）钝角三角形   （B）直角三角形   （C）锐角三角形    （D）不确定

 

【答案】

C

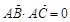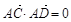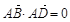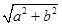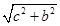【解析】∵，，，∴AB⊥AC，AC⊥AD，AB⊥AD，设 AB=a，AC=b，AD=c，则BC= ，CD= ，BD=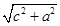，△BCD中，由余弦定理得cosB=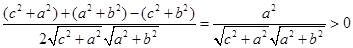，同理可证，cosC＞0，cosD＞0，∴B，C，D都是锐角，∴△BCD是锐角三角形，，故选C

 

练习册系列答案
相关题目
7、设A={x|x=2k，k∈Z}，B={x|x=2k+1，k∈Z}，C={x|x=2（k+1），k∈Z}，D={x|x=2k-1，k∈Z}，在A、B、C、D中，哪些集合相等，哪些集合的交集是空集？
（2013•长春一模）对于非空实数集A，记A*={y|?x∈A，y≥x}．设非空实数集合M、P满足：M⊆P，且若x＞1，则x∉P．现给出以下命题：
①对于任意给定符合题设条件的集合M、P，必有P*⊆M*；
②对于任意给定符合题设条件的集合M、P，必有M*∩P≠∅；
③对于任意给定符合题设条件的集合M、P，必有M∩P*=∅；
④对于任意给定符合题设条件的集合M、P，必存在常数a，使得对任意的b∈M*，恒有a+b∈P*，
其中正确的命题是（　　）
设P、Q为两个非空实数集合，定义集合P+Q={a+b|a∈P,b∈Q},若P={0,2,5},Q={1,2,6}，则P+Q中元素的个数是(    )

A.9               B.8            C.7             D.6

设全集为U，若M.N都是U的非空子集，且，则有（     ）

A、          B、

C、      D、

 

设是两个非空实数集合，定义集合.

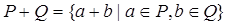若，则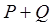中元素的个数是( 　)

A.  9       B. 8      C. 7      D.  6

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网