题目内容
(Ⅰ)求以点F1(-2,0),F2(2,0)分别为左右焦点,且经过点P(3,-2
)的椭圆的标准方程;
(Ⅱ)求中心在原点,焦点在坐标轴上,离心率为
,且经过点P(4,-
)的双曲线的方程.
| 6 |
(Ⅱ)求中心在原点,焦点在坐标轴上,离心率为
| 2 |
| 10 |
分析:(I)由椭圆的焦点坐标为F1(-2,0),F2(2,0)可得椭圆的焦点在x轴上,设椭圆的标准方程为
+
=1(a>b>0),将点P(3,-2
)的坐标代入,可得椭圆的标准方程;
(Ⅱ)由于焦点坐标可能以x轴上,也可能在y轴上,故应分为两种情况,结合双曲线的离心率为
,且经过点P(4,-
)构造方程,解方程可得双曲线的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
(Ⅱ)由于焦点坐标可能以x轴上,也可能在y轴上,故应分为两种情况,结合双曲线的离心率为
| 2 |
| 10 |
解答:解:(I)设椭圆的标准方程为
+
=1(a>b>0)
∵椭圆的焦点坐标为F1(-2,0),F2(2,0)
且经过点P(3,-2
)
故
解得a2=36,b2=32
故椭圆的标准方程为
+
=1
(II)∵双曲线的离心率为
,
故双曲线为等轴双曲线,即a=b
若焦点在x轴上,可设双曲线的标准方程为
-
=1
将点P(4,-
)代入得a2=6
故双曲线的标准方程为
-
=1
若焦点在y轴上,可设双曲线的标准方程为
-
=1
将点P(4,-
)代入得a2=-6(舍去)
综上双曲线的标准方程为
-
=1
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆的焦点坐标为F1(-2,0),F2(2,0)
且经过点P(3,-2
| 6 |
故
|
解得a2=36,b2=32
故椭圆的标准方程为
| x2 |
| 36 |
| y2 |
| 32 |
(II)∵双曲线的离心率为
| 2 |
故双曲线为等轴双曲线,即a=b
若焦点在x轴上,可设双曲线的标准方程为
| x2 |
| a2 |
| y2 |
| a2 |
将点P(4,-
| 10 |
故双曲线的标准方程为
| x2 |
| 6 |
| y2 |
| 6 |
若焦点在y轴上,可设双曲线的标准方程为
| y2 |
| a2 |
| x2 |
| a2 |
将点P(4,-
| 10 |
综上双曲线的标准方程为
| x2 |
| 6 |
| y2 |
| 6 |
点评:本题是中档题,考查椭圆方程和双曲线方程的求法,熟练掌握待定系数法求圆锥曲线标准方程的方法过程是解答的关键.

练习册系列答案
相关题目
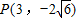 的椭圆的标准方程;
的椭圆的标准方程;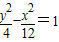 有相同渐近线,且经过点
有相同渐近线,且经过点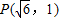 的双曲线的标准方程.
的双曲线的标准方程.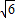 )的椭圆的标准方程;
)的椭圆的标准方程;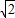 ,且经过点P(4,-
,且经过点P(4,-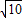 )的双曲线的方程.
)的双曲线的方程.