题目内容
自点A(-1,4)作圆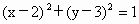 的切线l,求切线l的方程.
的切线l,求切线l的方程.
答案:y=4$3x+4y-13=0
解析:
解析:
|
解法 1:当直线l的斜率不存在时(即l垂直于x轴),不满足条件.当直线 l的斜率存在时,可设直线l的方程为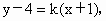 即 即
由平面几何知识可知,圆心 (2,3)到直线l的距离等于圆半径,故
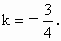
因此,所求直线 l的方程是y=4,或3x+4y-13=0.解法 2:当直线l的斜率不存在(即l垂直于x轴),不满足条件.当直线 l的斜率存在时,可设直线l的方程为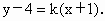
由于直线 l与圆相切,所以方程组 只有唯一解. 只有唯一解.
由方程组消去 y,得关于x的一元二次方程
由其判别式 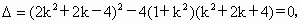
解之得 k=0,或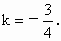
因此,所求直线 l的方程是y=4,或3x+4y-13=0. |

练习册系列答案
相关题目
自点
A(-1,4)作圆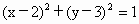 的切线,则切线长等于
的切线,则切线长等于
[ ]
|
A . |
B .3 |
|
C .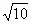 |
D .5 |
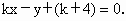

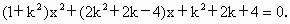
 的切线l,求切线l的方程.
的切线l,求切线l的方程. 的切线,则切线长等于
的切线,则切线长等于
