题目内容
已知Sn是正数数列{an}的前n项和,S12,S22、…、Sn2…,是以3为首项,以1为公差的等差数列;数列{bn}为无穷等比数列,其前四项之和为120,第二项与第四项之和为90.(1)求an、bn;(2)从数列{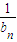 }中能否挑出唯一的无穷等比数列,使它的各项和等于
}中能否挑出唯一的无穷等比数列,使它的各项和等于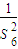 .若能的话,请写出这个数列的第一项和公比?若不能的话,请说明理由.
.若能的话,请写出这个数列的第一项和公比?若不能的话,请说明理由.
【答案】分析:(1)根据{Sn2}是以3为首项,以1为公差的等差数列求出通项公式,得到Sn,然后根据an=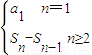 进行求解,根据{bn}是等比数列,求出首项和公比即可求出bn;
进行求解,根据{bn}是等比数列,求出首项和公比即可求出bn;
(2)设可以挑出一个无穷等比数列{cn},首项为c1=( )p,公比为(
)p,公比为( )k,(p、k∈N),它的各项和等于
)k,(p、k∈N),它的各项和等于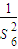 =
= ,建立等式关系,讨论p和k的大小,从而求出满足条件的等比数列.
,建立等式关系,讨论p和k的大小,从而求出满足条件的等比数列.
解答:解:(1){Sn2}是以3为首项,以1为公差的等差数列;所以Sn2=3+(n-1)=n+2
因为an>0,所以Sn=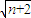 (n∈N)(2分)
(n∈N)(2分)
当n≥2时,an=Sn-Sn-1=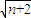 -
-
又a1=S1=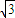 ,所以an=
,所以an=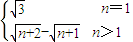 (n∈N) (4分)
(n∈N) (4分)
设{bn}的首项为b1,公比为q,则有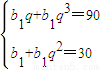 (6分)
(6分)
所以 ,所以bn=3n(n∈N)(8分)
,所以bn=3n(n∈N)(8分)
(2)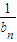 =(
=( )n,设可以挑出一个无穷等比数列{cn},首项为c1=(
)n,设可以挑出一个无穷等比数列{cn},首项为c1=( )p,公比为(
)p,公比为( )k,(p、k∈N),它的各项和等于
)k,(p、k∈N),它的各项和等于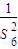 =
= ,(10分)
,(10分)
则有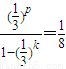 ,所以(
,所以( )p=
)p= [1-(
[1-( )k],(12分)
)k],(12分)
当p≥k时3p-3p-k=8,即3p-k(3k-1)=8,因为p、k∈N,所以只有p-k=0,k=2时,
即p=k=2时,数列{cn}的各项和为 . (14分)
. (14分)
当p<k时,3k-1=8.3k-p,因为k>p右边含有3的因数,而左边非3的倍数,不存在p、k∈N,
所以唯一存在等比数列{cn},首项为 ,公比为
,公比为 ,使它的各项和等于
,使它的各项和等于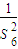 .(16分)
.(16分)
点评:本题主要考查了数列的通项公式,以及等比数列的求和等有关知识,属于中档题.
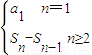 进行求解,根据{bn}是等比数列,求出首项和公比即可求出bn;
进行求解,根据{bn}是等比数列,求出首项和公比即可求出bn;(2)设可以挑出一个无穷等比数列{cn},首项为c1=(
 )p,公比为(
)p,公比为( )k,(p、k∈N),它的各项和等于
)k,(p、k∈N),它的各项和等于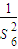 =
= ,建立等式关系,讨论p和k的大小,从而求出满足条件的等比数列.
,建立等式关系,讨论p和k的大小,从而求出满足条件的等比数列.解答:解:(1){Sn2}是以3为首项,以1为公差的等差数列;所以Sn2=3+(n-1)=n+2
因为an>0,所以Sn=
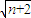 (n∈N)(2分)
(n∈N)(2分)当n≥2时,an=Sn-Sn-1=
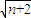 -
-
又a1=S1=
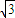 ,所以an=
,所以an=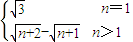 (n∈N) (4分)
(n∈N) (4分)设{bn}的首项为b1,公比为q,则有
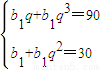 (6分)
(6分)所以
 ,所以bn=3n(n∈N)(8分)
,所以bn=3n(n∈N)(8分)(2)
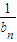 =(
=( )n,设可以挑出一个无穷等比数列{cn},首项为c1=(
)n,设可以挑出一个无穷等比数列{cn},首项为c1=( )p,公比为(
)p,公比为( )k,(p、k∈N),它的各项和等于
)k,(p、k∈N),它的各项和等于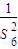 =
= ,(10分)
,(10分)则有
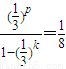 ,所以(
,所以( )p=
)p= [1-(
[1-( )k],(12分)
)k],(12分)当p≥k时3p-3p-k=8,即3p-k(3k-1)=8,因为p、k∈N,所以只有p-k=0,k=2时,
即p=k=2时,数列{cn}的各项和为
 . (14分)
. (14分)当p<k时,3k-1=8.3k-p,因为k>p右边含有3的因数,而左边非3的倍数,不存在p、k∈N,
所以唯一存在等比数列{cn},首项为
 ,公比为
,公比为 ,使它的各项和等于
,使它的各项和等于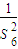 .(16分)
.(16分)点评:本题主要考查了数列的通项公式,以及等比数列的求和等有关知识,属于中档题.

练习册系列答案
相关题目