题目内容
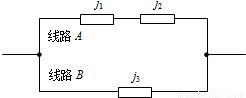
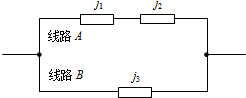 由三个电子元件j1,j2,j3组成的线路系统如图所示,每个电子元件能正常工作的概率都是t (0<t<1).
由三个电子元件j1,j2,j3组成的线路系统如图所示,每个电子元件能正常工作的概率都是t (0<t<1).(1)求该线路系统正常工作的概率P;
(2)试问函数P(t)在区间(0,1)上是否存在最值?
分析:(1)“该线路系统正常工作”即“线路A、线路B至少一条正常工作”,其对立事件为“线路A、线路B都不能正常工作”,由于各线路能否正常工作相互独立,“线路A、线路B都不能正常工作”的概率为“线路A不能正常工作”的概率乘以“线路B不能正常工作”的概率.
(2)先求函数P(t)的导函数,研究此函数在区间(0,1)的单调性,再根据单调性判断函数有无最值
(2)先求函数P(t)的导函数,研究此函数在区间(0,1)的单调性,再根据单调性判断函数有无最值
解答:解:(1)记线路A、线路B正常工作的概率分别为P(A)、P(B)
P(A)=P(j1)P(j2)=t2 P(B)=t
系统正常工作的概率P=1-P(
) • P(
)=1-(1-t2)(1-t)=-t3+t2+t
(2)P'(t)=-3t2+2t+1=-(3t+1)(t-1)
∵当0<t<1时,P'(t)>0
∴P(t)在(0,1)上单调递增
∴P(t)在开区间(0,1)上不存在最值
P(A)=P(j1)P(j2)=t2 P(B)=t
系统正常工作的概率P=1-P(
. |
| A |
. |
| B |
(2)P'(t)=-3t2+2t+1=-(3t+1)(t-1)
∵当0<t<1时,P'(t)>0
∴P(t)在(0,1)上单调递增
∴P(t)在开区间(0,1)上不存在最值
点评:本题综合考察了独立事件同时发生的概率,对立事件的概率,导数应用等知识,解题时要辨明事件关系,准确判断

练习册系列答案
相关题目
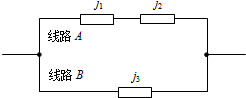 由三个电子元件j1,j2,j3组成的线路系统如图所示,每个电子元件能正常工作的概率都是t (0<t<1).
由三个电子元件j1,j2,j3组成的线路系统如图所示,每个电子元件能正常工作的概率都是t (0<t<1).