题目内容
14.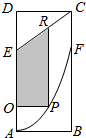 某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.
某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.(1)求曲线AF与AB,BF所围成区域的面积;
(2)求该公园的最大面积.
分析 (1)以A为原点,AB所在直线为x轴建立平面直角坐标系,设出抛物线方程y=ax2(a>0),把F的坐标代入求得a值得答案;
(2)由题意求出E,C的坐标,得到直线EC的方程,设P(x,x2)(0<x<2),由梯形面积公式得到公园的面积S,利用导数求得公园的最大面积.
解答  解:(1)以A为原点,AB所在直线为x轴建立平面直角坐标系,
解:(1)以A为原点,AB所在直线为x轴建立平面直角坐标系,
设曲线AF所在抛物线方程为y=ax2(a>0),
∵抛物线过F(2,4),∴4=a×22,得a=1.
∴AF所在抛物线方程为y=x2.
则曲线AF与AB,BF所围成区域的面积$S{=∫}_{0}^{2}{x}^{2}dx=\frac{1}{3}{x}^{2}{|}_{0}^{2}=\frac{8}{3}$ km2;
(2)又E(0,4),C(2,6),则EC所在直线方程为y=x+4.
设P(x,x2)(0<x<2),则PO=x,OE=4-x2,PR=4+x-x2,
∴公园的面积S=$\frac{1}{2}(4-{x}^{2}+4+x-{x}^{2})•x=-{x}^{3}+\frac{1}{2}{x}^{2}+4x$(0<x<2).
∴S′=-3x2+x+4,
令S′=0,得x=$\frac{4}{3}$或x=-1(舍去).
当x变化时,S′和S的变化情况如下表:
| x | (0,$\frac{4}{3}$) | $\frac{4}{3}$ | ($\frac{4}{3},2$) |
| S′ | + | 0 | - |
| S | 单调递增 | 极大值$\frac{104}{27}$ | 单调递减 |
故该公园的最大面积为$\frac{104}{27}$.
点评 本题考查简单的数学建模思想方法,考查了抛物线方程的求法,训练了利用定积分求曲边梯形的面积,考查利用导数求函数的极值,是中档题.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
5.下列函数完全相同的是( )
| A. | f(x)=x,g(x)=x2 | B. | f(x)=x,g(x)=$\root{3}{x^3}$ | C. | f(x)=x,g(x)=$\sqrt{x}$ | D. | f(x)=$\sqrt{x^2}g(x)=\sqrt{x}$ |
2.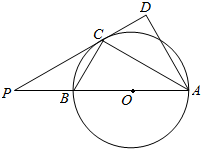 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.
如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.
(1)求证:PC2=PA•PB;
(2)若3AC=4BC,⊙O的直径为7,求线段PC的长.
 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.
如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.(1)求证:PC2=PA•PB;
(2)若3AC=4BC,⊙O的直径为7,求线段PC的长.
6.设集合A={x|0<x<4},B={x|x<a}若A⊆B,则实数a的取值范围是( )
| A. | {a|a≤0} | B. | {a|0<a≤4} | C. | {a|a≥4} | D. | {a|0<a<4} |
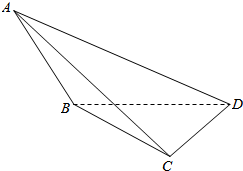 如图在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=$\sqrt{3}$,BD=CD=1,另一个侧面是正三角形
如图在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=$\sqrt{3}$,BD=CD=1,另一个侧面是正三角形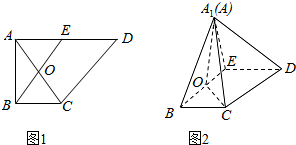 如图1,在直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=$\frac{1}{2}$AD,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2,
如图1,在直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=$\frac{1}{2}$AD,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2,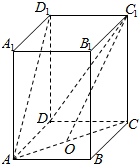 如图,在长方体中ABCD-A1B1C1D1,AB=3,BC=AA1=4,点O是AC的中点.
如图,在长方体中ABCD-A1B1C1D1,AB=3,BC=AA1=4,点O是AC的中点.