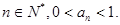题目内容
设曲线 在点
在点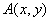 处的切线斜率为
处的切线斜率为 ,且
,且 ,对一切实数
,对一切实数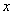 ,不等式
,不等式 恒成立
恒成立 .
.
(1)
求 的值;
的值;
(2)
求函数 的表达式;
的表达式;
(3)
求证: .
.
【答案】
(1)k(1)=1(2)k(x)=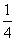 x2+
x2+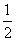 x+
x+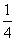 =
=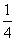 (x+1)2;
(x+1)2;
(3)第二问的基础上,利用均值不等式放缩来得到证明。
【解析】
试题分析:解:(1)根据题意,对一切实数x,不等式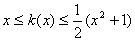 恒成立,则当x=1时,有1≤k(1)≤
恒成立,则当x=1时,有1≤k(1)≤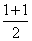 =1,即1≤k(1)≤1,则k(1)=1
=1,即1≤k(1)≤1,则k(1)=1
(2)对曲线方程求导可得k(x)=ax2+bx+c, k(-1)=0,则a-b+c=0------①由(1)得,k(1)=1,则a+b+c=1------②由①②得a+c=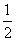 ,b=
,b=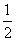 ;则k(x)=ax2+
;则k(x)=ax2+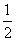 x+c,又由x≤k(x)≤
x+c,又由x≤k(x)≤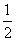 (x2+1)恒成立可得,
ax2-
(x2+1)恒成立可得,
ax2-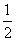 x+c≥0且(2a-1)x2+1x+(2c-1)≤0恒成立,由ax2+
x+c≥0且(2a-1)x2+1x+(2c-1)≤0恒成立,由ax2+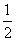 x+c≥0恒成立可得a>0,
x+c≥0恒成立可得a>0,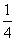 ≤4ac,由(2a-1)x2+1x+(2c-1)≤0恒成立可得(2a-1)<0,1≤4(2a-1)(2c-1)得0<a<
≤4ac,由(2a-1)x2+1x+(2c-1)≤0恒成立可得(2a-1)<0,1≤4(2a-1)(2c-1)得0<a<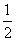 ,且
,且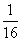 ≤ac≤
≤ac≤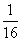
ac=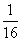 ,且a+c=
,且a+c=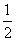 ,则a=c=
,则a=c=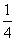 ,则k(x)=
,则k(x)=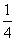 x2+
x2+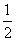 x+
x+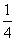 =
=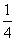 (x+1)2;
(x+1)2;
证明:(3)由(2)可得k(x)=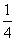 (x+1)2,则
(x+1)2,则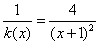 >
>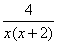 =2(
=2(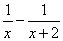 ),即
),即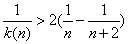 );
);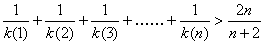 则即不等式可证.
则即不等式可证.
考点:函数的恒成立、曲线的切线方程
点评:本题综合考查函数的恒成立问题、曲线的切线方程以及放缩法证明不等式,难度较大;解(Ⅱ)题时要注意二次函数大于等于0恒成立的条件.

练习册系列答案
相关题目
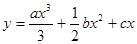 在点
在点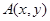 处的切线斜率为
处的切线斜率为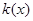 ,且
,且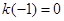 .对一切实数
.对一切实数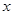 ,不等式
,不等式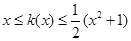 恒成立(
恒成立(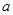 ≠0).
≠0).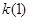 的值;
的值;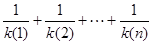 >
>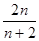 .
. 在点
在点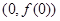 处的切线斜率为
处的切线斜率为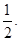
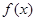 的极值;
的极值;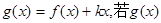 在(-∞,1)上是增函数,求实数
在(-∞,1)上是增函数,求实数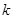 的取值范围;
的取值范围;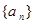 满足
满足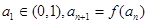 ,求证:对一切
,求证:对一切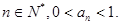
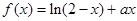 在点
在点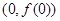 处的切线斜率为
处的切线斜率为
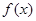 的极值;
的极值;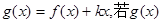 在(-∞,1)上是增函数,求实数
在(-∞,1)上是增函数,求实数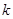 的取值范围;
的取值范围;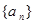 满足
满足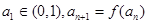 ,求证:对一切
,求证:对一切