题目内容
在下列各点中,不在不等式2x+3y<5表示的平面区域内的点为( )A.(0,1)
B.(1,0)
C.(0,2)
D.(2,0)
【答案】分析:分别把A,B,C,D四个点的坐标代入不等式2x+3y<5进行判断,能够求出结果.
解答:解:把(0,1)代入不等式2x+3y<5,
得3<5,成立,∴点A在不等式2x+3y<5表示的平面区域内;
把(1,0)代入不等式2x+3y<5,
得2<5,成立,∴点B在不等式2x+3y<5表示的平面区域内;
把(0,2)代入不等式2x+3y<5,
得6<5,不成立,∴点C不在不等式2x+3y<5表示的平面区域内;
把(2,0)代入不等式2x+3y<5,
得4<5,成立,∴点D在不等式2x+3y<5表示的平面区域内.
故选C.
点评:本题考查二元一次不等式组表示的平面区域的应用,是基础题.解题时要认真审题,仔细解答.
解答:解:把(0,1)代入不等式2x+3y<5,
得3<5,成立,∴点A在不等式2x+3y<5表示的平面区域内;
把(1,0)代入不等式2x+3y<5,
得2<5,成立,∴点B在不等式2x+3y<5表示的平面区域内;
把(0,2)代入不等式2x+3y<5,
得6<5,不成立,∴点C不在不等式2x+3y<5表示的平面区域内;
把(2,0)代入不等式2x+3y<5,
得4<5,成立,∴点D在不等式2x+3y<5表示的平面区域内.
故选C.
点评:本题考查二元一次不等式组表示的平面区域的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
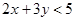 表示的平面区域内的点为(
)
表示的平面区域内的点为(
) B.
B.  C.
C.  D.
D. 