题目内容
8、在下面的程序框图中,输入f0(x)=cosx,(其中 (sinx)′=cosx,(cosx)′=-sinx)则输出的是

sinx
.
分析:由题意f0(x)=cosx,f1(x)=f0′(x)=-sinx,f2(x)=-cosx,f3(x)=sinx,f4(x)=cosx,以此类推,结构循环出现,周期为4.
由程序框图可知输出的是f2007(x),利用周期性求解即可.
由程序框图可知输出的是f2007(x),利用周期性求解即可.
解答:解:由题意f0(x)=cosx,f1(x)=f0′(x)=-sinx,f2(x)=-cosx,f3(x)=sinx,f4(x)=cosx,
以此类推,结构循环出现,周期为4.
由程序框图可知输出的是f2007(x),
因为f2007(x)=f3(x)=sinx.所以输出结果为sinx
故答案为:sinx
以此类推,结构循环出现,周期为4.
由程序框图可知输出的是f2007(x),
因为f2007(x)=f3(x)=sinx.所以输出结果为sinx
故答案为:sinx
点评:本题考查循环结构的程序框图、归纳推理、三角函数的导数等知识,发现周期性规律是解决本题的关键.

练习册系列答案
相关题目
 在下面的程序框图中,输出的数s=( )
在下面的程序框图中,输出的数s=( )
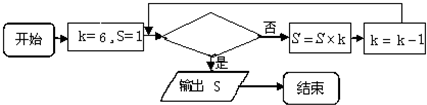
 是
是 的函数,记为
的函数,记为 ,则
,则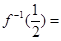 .
.