题目内容
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图1所示的一条折线表示:西红柿的种植成本与上市时间的关系用图2所示的抛物线表示。(注:市场售价和种植成本的单位:元/102kg,时间单位:天)
(1)写出图1表示的市场售价与时间的函数关系式P=f(t);写出图2表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?为多少?
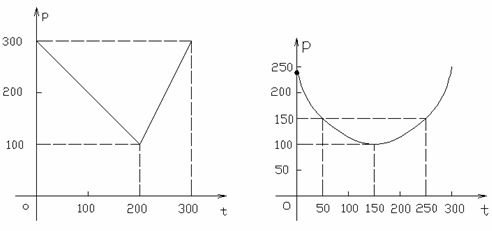
图1 图2
【答案】
解:(1)由图1可得市场售价与时间的函数关系为:f(t)=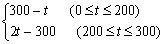 …2′
…2′
由图2可得种植成本与时间的函数关系为:g(t)=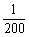 (t-150)2+100 (0
(t-150)2+100 (0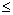 t
t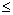 300)………4′
300)………4′
(2)设t时刻的纯收益为h(t),则由题意得h(t)=f(t)-g(t),
即h(t)=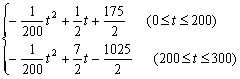 ………………………………6′
………………………………6′
当0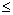 t
t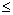 200时,配方整理,得h(t)= -
200时,配方整理,得h(t)= -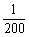 (t-50)2+100
(t-50)2+100
∴当t=50时,h(t)取得区间[0,200]上的最大值100;…………………………………8′
当200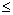 t
t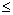 300时,配方整理,得h(t)= -
300时,配方整理,得h(t)= -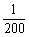 (t-350)2+100
(t-350)2+100
∴t=300时,h(t)取得区间(200,300]上的最大值87.5;………………………………10′
综上可知h(t)在区间[0,300]上可以取到最大值100,此时,t=50 ,即从二月一日开始的第50天时,上市的西红柿收益最大100。…………………………………………………12′

练习册系列答案
相关题目



