题目内容
一台设备由三大部件组成,在设备运转中,各部件需要调整的概率相应为0.10,0.20和0.30.假设各部件的状态相互独立,以ξ表示同时需要调整的部件数,试求ξ的数学期望Eξ和方差Dξ.
【答案】
0.6,0.46。
【解析】
试题分析:解:设Ai={部件i需要调整}(i=1,2,3),则P(A1)=0.1,P(A2)=0.2,P(A3)=0.3.
由题意,ξ有四个可能值0,1,2,3.由于A1,A2,A3相互独立,可见
P(ξ=0)=P(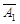
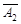
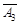 )=0.9×0.8×0.7=0.504;
)=0.9×0.8×0.7=0.504;
P(ξ=1)=P(A1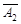
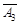 )+P(
)+P(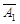 A2
A2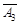 )+P(
)+P(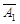
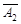 A3)=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398;
A3)=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398;
P(ξ=2)=P(A1A2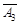 )+P(A1
)+P(A1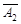 A3)+P(
A3)+P(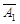 A2A3)=0.1×0.2×0.7+0.1×0.8×0.3+0.9×0.2×0.3=0.092;
A2A3)=0.1×0.2×0.7+0.1×0.8×0.3+0.9×0.2×0.3=0.092;
P(ξ=3)=P(A1A2A3)=0.1×0.2×0.3=0.006.
∴Eξ=1×0.398+2×0.092+3×0.006=0.6,
Dξ=Eξ2-(Eξ)2=1×0.398+4×0.092+9×0.006-0.62=0.82-0.36=0.46.
考点:本题主要考查离散型随机变量的期望、方差的计算。
点评:从相互独立事件计算入手,利用期望、方差的计算公式,综合性较强,对计算能力要求较高。

练习册系列答案
相关题目