题目内容
莆田十中高三(1)研究性学习小组对函数f(x)=
的性质进行了探究,小组长收集到了以下命题:
下列说法中正确命题的序号是
①f(x)是偶函数; ②f(x)是周期函数;
③f(x)在区间(0,π)上的单调递减; ④f(x)没有值最大值.
| sinx | x |
下列说法中正确命题的序号是
①③④
①③④
.(填出所有正确命题的序号)①f(x)是偶函数; ②f(x)是周期函数;
③f(x)在区间(0,π)上的单调递减; ④f(x)没有值最大值.
分析:直接利用f(-x)与f(x)之间的关系即可判断①是否成立;
借助于导函数值的正负即可判断出③是否成立;
根据y=sinx是周期为2π的函数,函数值每过2π重复出现,但y=x是一单调递增函数即可判断出②④.
借助于导函数值的正负即可判断出③是否成立;
根据y=sinx是周期为2π的函数,函数值每过2π重复出现,但y=x是一单调递增函数即可判断出②④.
解答:解:因为函数f(x)=
,
∴f(-x)=
=
=
=f(x).即f(x)是偶函数;①成立.
又f′(x)=
,
令g(x)=xcosx+sinx,得g′(x)=-xsinx,在(0,π)上,g′(x)<0恒成立,故g(x)max<g(0)=0.
∴f′(x)<0恒成立.
∴f(x)在区间(0,π)上的单调递减; 即③成立.
又∵y=sinx是周期为2π的函数,函数值每过2π重复出现,但y=x是一单调递增函数,
所以:f(x)不是周期函数;且f(x)没有值最大值,即②不成立,④成立.
故答案为:①③④.
| sinx |
| x |
∴f(-x)=
| sin(-x) |
| -x |
| -sinx |
| -x |
| sinx |
| x |
又f′(x)=
| xcosx+sinx |
| x2 |
令g(x)=xcosx+sinx,得g′(x)=-xsinx,在(0,π)上,g′(x)<0恒成立,故g(x)max<g(0)=0.
∴f′(x)<0恒成立.
∴f(x)在区间(0,π)上的单调递减; 即③成立.
又∵y=sinx是周期为2π的函数,函数值每过2π重复出现,但y=x是一单调递增函数,
所以:f(x)不是周期函数;且f(x)没有值最大值,即②不成立,④成立.
故答案为:①③④.
点评:本题主要考查函数的奇偶性的判断以及导函数在研究函数单调性中的应用问题.在判断函数的奇偶性时,一般是先看定义域,再看f(-x)与f(x)之间的关系,当f(-x)=f(x)时为偶函数,当f(-x)=-f(x)时为奇函数.

练习册系列答案
相关题目
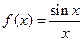 的性质进行了探究,
的性质进行了探究,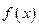 是偶函数; ②
是偶函数; ②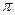 )上的单调递减; ④
)上的单调递减; ④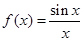 的性质进行了探究,
的性质进行了探究,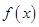 是偶函数;
②
是偶函数;
②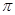 )上的单调递减; ④
)上的单调递减; ④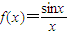 的性质进行了探究,小组长收集到了以下命题:
的性质进行了探究,小组长收集到了以下命题: