题目内容
已知不等式a≤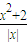
对x取一切负数恒成立，则a的取值范围是
【答案】分析：本题为不等式恒成立问题，转化为求函数f（x）=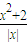
（x＜0）的最小值问题，可考虑用基本不等式求解．
解答：解：不等式a≤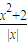
对x取一切负数恒成立，只要a≤（
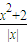）min（x＜0）．
令f（x）=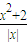
，x＜0时，f（x）=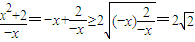
当且仅当
时“=”成立
所以f（x）的最小值为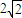
∴a≤2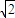
．
故选A≤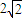
点评：本题为不等式恒成立问题，不等式恒成立问题往往转化为求函数的最值问题，基本不等式是求函数最值的一种常用方法，属常规题型．
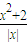（x＜0）的最小值问题，可考虑用基本不等式求解．解答：解：不等式a≤
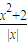对x取一切负数恒成立，只要a≤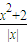（）min（x＜0）．令f（x）=
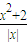，x＜0时，f（x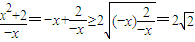）=当且仅当
时“=”成立所以f（x）的最小值为
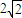∴a≤2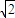．故选A≤
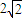
点评：本题为不等式恒成立问题，不等式恒成立问题往往转化为求函数的最值问题，基本不等式是求函数最值的一种常用方法，属常规题型．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
对x取一切负数恒成立,则a的取值范围是_____________.
对x取一切负数恒成立,则a的取值范围是___________________.
对x取一切负数恒成立，则a的取值范围是____________.