题目内容

已知平面上三点A，B，C满足|
AB
|=5，|
BC
|=12，|
CA
|=13，则
AB
•
BC
+
BC
•
CA
+
CA
•
AB
的值等于
-169
-169
．
分析：由平面上三点A，B，C满足|
AB
|=5，|
BC
|=12，|
CA
|=13，可得|
AB
|2+|
BC
|2=|
CA
|2，利用勾股定理的逆定理得∠ABC=90°．如图所示，可得cosA=
5
13
，cosC=
12
13
．再利用数量积可得
AB
•
BC
+
BC
•
CA
+
CA
•
AB
=0+|
BC
| |
CA
|cos(π-C)+|
CA
| |
AB
| cos(π-A)，代入计算即可．
解答：解：∵平面上三点A，B，C满足|
AB
|=5，|
BC
|=12，|
CA
|=13，
∴|
AB
|2+|
BC
|2=|
CA
|2．
∴∠ABC=90°．
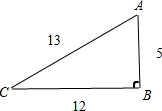
如图所示，cosA=
5
13
，cosC=
12
13
．
∴
AB
•
BC
+
BC
•
CA
+
CA
•
AB

=0+|
BC
| |
CA
|cos(π-C)+|
CA
| |
AB
| cos(π-A)
=12×13×(-
12
13
)+13×5×(-
5
13
)
=-169．
故答案为-169．
点评：熟练掌握勾股定理的逆定理、三角函数、数量积运算是解题的关键．注意向量的夹角不要找错．
练习册系列答案
相关题目
已知平面上三点A、B、C满足|
AB
|=2，|
BC
|=1，|
CA
|=
3
，则
AB
•
BC
+
BC
•
CA
+
CA
•
AB
的值等于
 
．
已知平面上三点A、B、C满足|
AB
|=3，|
BC
|=4，|
CA
|=5，则
AB
•
BC
+
BC
•
CA
+
CA
•
AB
的值等于（　　）
A、25B、-25
C、24D、-24
已知平面上三点A，B，C在一条直线上，
OA
=(-2，m)，
OB
=(n，1)，
OC
=(5，-1)，且
OA
⊥
OB
，求实数m，n的值．
已知平面上三点A、B、C满足|
AB
|=6，|
BC
|=8，|
CA
|=10，则
AB
•
BC
+
BC
•
CA
+
CA
•
AB
的值等于
-100
-100
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网