题目内容
圆C过点(0,-1),圆心在y轴的正半轴上,且与圆(x-4)2+(y-4)2=9外切.
(Ⅰ)求圆C的方程;
(Ⅱ)直线l过点(0,2)交圆C于A、B两点,若坐标原点O在以AB为直径的圆内,求直线l的倾斜角α的取值范围.
(Ⅰ)求圆C的方程;
(Ⅱ)直线l过点(0,2)交圆C于A、B两点,若坐标原点O在以AB为直径的圆内,求直线l的倾斜角α的取值范围.
分析:(Ⅰ)设出圆的方程,利用圆C过点(0,-1),圆与圆(x-4)2+(y-4)2=9外切,建立方程,即可求圆C的方程;
(Ⅱ)设直线l的方程为,求出以AB为直径的圆半径R,原点与l的距离d',利用原点O在以AB为直径的圆内,可得d'<R,从而可求直线l的倾斜角α的取值范围.
(Ⅱ)设直线l的方程为,求出以AB为直径的圆半径R,原点与l的距离d',利用原点O在以AB为直径的圆内,可得d'<R,从而可求直线l的倾斜角α的取值范围.
解答:解:(Ⅰ)圆C的圆心在y轴的正半轴上,故可设方程为x2+(y-b)2=r2,b>0,r>0
由条件知 (-1-b)2=r2(1)
∵圆与圆(x-4)2+(y-4)2=9外切,∴两个圆心间的距离等于两个半径之和,
∴(0-4)2+(b-4)2=(r+3)2(2)
由(1)(2)解得b=1,r=2
从而圆C的方程为x2+(y-1)2=4;
(Ⅱ)设直线l的方程为y=kx+2,即kx-y+2=0
∵C与l的距离d=
,∴以AB为直径的圆半径R=
=
∵原点O在以AB为直径的圆内,原点与l的距离d'=
∴d'<R,即
<
∴k<-
或k>
.
斜率不存在时也成立
∴直线l的倾斜角α的取值范围为(arctan
,π-arctan
).
由条件知 (-1-b)2=r2(1)
∵圆与圆(x-4)2+(y-4)2=9外切,∴两个圆心间的距离等于两个半径之和,
∴(0-4)2+(b-4)2=(r+3)2(2)
由(1)(2)解得b=1,r=2
从而圆C的方程为x2+(y-1)2=4;
(Ⅱ)设直线l的方程为y=kx+2,即kx-y+2=0
∵C与l的距离d=
| 1 | ||
|
| 4-d2 |
|
∵原点O在以AB为直径的圆内,原点与l的距离d'=
| 2 | ||
|
∴d'<R,即
| 2 | ||
|
|
∴k<-
| 1 |
| 2 |
| 1 |
| 2 |
斜率不存在时也成立
∴直线l的倾斜角α的取值范围为(arctan
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查圆的标准方程,考查点与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
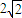 则圆C的标准方程为 .
则圆C的标准方程为 .