题目内容
在锐角三角形中,三个内角A、B、C的对边分别为a、b、c,满足条件sin22B+sin2BsinB+cos2B=1.
(Ⅰ)求∠B的值;
(Ⅱ)若b=3,求a+c的最大值.
(Ⅰ)求∠B的值;
(Ⅱ)若b=3,求a+c的最大值.
分析:(1)利用二倍角公式对sin22B+sin2BsinB+cos2B=1进行化简,最后求得cosB,进而求得B.
(Ⅱ)由余弦定理可得 b2=9=(a+c)2-3ac≥(a+c)2-
(a+c)2=(
)2,由此求得a+c的最大值.
(Ⅱ)由余弦定理可得 b2=9=(a+c)2-3ac≥(a+c)2-
| 3 |
| 4 |
| a+c |
| 2 |
解答:解:(1)∵sin22B+sin2BsinB+cos2B=1,∴4sin2Bcos2B+2sin2BcosB-2sin2B=0,
即2sin2B(2cosB-1)(cosB+1)=0.
又△ABC为锐角三角形,∴2cosB-1=0,即∠B=
.
(Ⅱ)若b=3,由上可得∠B=
,由余弦定理可得 cosB=
=
,
∴b2=9=a2+c2-2ac×
=(a+c)2-3ac≥(a+c)2-
(a+c)2=(
)2,
∴a+c≤6,即a+c的最大值为6.
即2sin2B(2cosB-1)(cosB+1)=0.
又△ABC为锐角三角形,∴2cosB-1=0,即∠B=
| π |
| 3 |
(Ⅱ)若b=3,由上可得∠B=
| π |
| 3 |
| a2+c 2-b 2 |
| 2ac |
| 1 |
| 2 |
∴b2=9=a2+c2-2ac×
| 1 |
| 2 |
| 3 |
| 4 |
| a+c |
| 2 |
∴a+c≤6,即a+c的最大值为6.
点评:本题主要考查了余弦定理、二倍角公式的应用.在求最值的问题上,对于二次函数,常用配方法来求,属于中档题.

练习册系列答案
相关题目
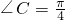 ,求∠A的大小.
,求∠A的大小. 的取值范围.
的取值范围.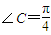 ,求∠A的大小.
,求∠A的大小.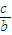 的取值范围.
的取值范围.